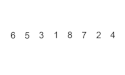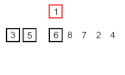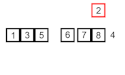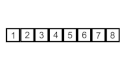Sortowanie przez wstawianie

Sortowanie przez wstawianie

Przykład działania sortowania przez wstawianie
Rodzaj	Sortowanie
Struktura danych	Tablica, lista
Złożoność
Czasowa	${\displaystyle O(n^{2})}$
Pamięciowa	${\displaystyle O(1)}$

Sortowanie przez wstawianie (ang. Insert Sort, Insertion Sort) – jeden z najprostszych algorytmów sortowania, którego zasada działania odzwierciedla sposób w jaki ludzie ustawiają karty – kolejne elementy wejściowe są ustawiane na odpowiednie miejsca docelowe^[1]. Jest efektywny dla niewielkiej liczby elementów, jego złożoność wynosi O(n²)^[1]. Pomimo tego, że jest znacznie mniej wydajny od algorytmów takich jak quicksort czy heapsort, posiada pewne zalety:

• liczba wykonanych porównań jest zależna od liczby inwersji w permutacji, dlatego algorytm jest wydajny dla danych wstępnie posortowanych^[2],
• jest wydajny dla zbiorów o niewielkiej liczebności^[1],
• jest stabilny^[1].

Istnieje modyfikacja algorytmu, pozwalająca zmniejszyć liczbę porównań. Zamiast za każdym razem iterować po już posortowanym fragmencie (etap wstawiania elementu), można posłużyć się wyszukiwaniem binarnym. Pozwala to zmniejszyć liczbę porównań do O(nlogn), nie zmienia się jednak złożoność algorytmu, ponieważ liczba przesunięć elementów to nadal O(n²)^[3].

Schemat działania algorytmu^[1]

Przykład działania

1. Utwórz zbiór elementów posortowanych i przenieś do niego dowolny element ze zbioru nieposortowanego.
2. Weź dowolny element ze zbioru nieposortowanego.
3. Wyciągnięty element porównuj z kolejnymi elementami zbioru posortowanego, póki nie napotkasz elementu równego lub elementu większego (jeśli chcemy otrzymać ciąg niemalejący) lub nie znajdziemy się na początku/końcu zbioru uporządkowanego.
4. Wyciągnięty element wstaw w miejsce, gdzie skończyłeś porównywać.
5. Jeśli zbiór elementów nieuporządkowanych jest niepusty, wróć do punktu 2.

Algorytm – pseudokod

Poniższy kod przedstawia algorytm zapisany w pseudokodzie, gdzie^[4]:

• A – tablica danych przeznaczonych do posortowania (indeksowana od 1 do n),
• n – liczba elementów w tablicy A.

0. Insert_sort(A, n)

1.  for i=2 to n :
2       # Wstaw A[i] w posortowany ciąg A[1 ... i-1]
3.      wstawiany_element = A[i]
4.      j = i - 1
5.      while i>0 and A[j]>wstawiany_element:
6.          A[j + 1] = A[j]
7.          j = j - 1
8.          A[j + 1] = wstawiany_element

Analiza algorytmu

Złożoność

Niech δ(i) oznacza liczba sprawdzeń warunku pętli (5.) w i-tym przebiegu pętli (1.). Wtedy:

• instrukcja 1. jest wykonana n razy
• instrukcja 2. jest wykonana n-1 razy
• instrukcja 3. jest wykonana n-1 razy (komentarz oznaczony przez >)
• instrukcja 4. jest wykonana n-1 razy
• instrukcja 5. jest wykonana ${\displaystyle \sum _{i=2}^{n}\delta (i)}$ razy
• instrukcja 6. jest wykonana ${\displaystyle \sum _{i=2}^{n}\delta (i)-1}$ razy
• instrukcja 7. jest wykonana ${\displaystyle \sum _{i=2}^{n}\delta (i)-1}$ razy
• instrukcja 8. jest wykonana n-1 razy

Jeżeli przez c₁, c₂, ..., c₈ oznaczymy czas pojedynczego wywołania instrukcji 1,2, ... 8, to całkowity czas wykonania algorytmu sortowania przez wstawianie będzie równy:

T(n) = c₁n + (c₂+c₃+c₄+c₈)(n-1) + ${\displaystyle \sum _{i=2}^{n}\delta (i)}$ c₅ + (${\displaystyle \sum _{i=2}^{n}\delta (i)-1}$)c₆ + (${\displaystyle \sum _{i=2}^{n}\delta (i)-1}$)c₇

Przypadek optymistyczny

Gdy tablica danych wejściowych jest uporządkowana rosnąco, to w każdym przebiegu pętli (1.) przy pierwszym sprawdzeniu warunków pętli (5.) zachodzi A[j]<klucz - pętla (5.) nie zostaje wykonana ani razu, a więc liczba sprawdzeń warunku pętli (5.) δ(i) wynosi 1 dla wszystkich j od 1 do n. Całkowity czas T(n) = (c₁ + c₂ + c₄ + c₅ + c₈)n - (c₂ + c₄ + c₅ + c₈) wykonania algorytmu jest więc wyrażony funkcją liniową, z czego wynika, że dla posortowanych tablic o długości n algorytm insert sort działa w czasie O(n).

Przypadek pesymistyczny

Gdy tablica danych wejściowych jest uporządkowana malejąco, w każdym przebiegu pętli (1.) przy sprawdzaniu warunków pętli (5.) zachodzi A[j]>klucz - pętla (5.) w każdym i-tym przebiegu pętli (1.) jest wywoływana i-1 razy. Po podstawieniu do wzoru na T(n): δ(i) = i, otrzymuje się kwadratową złożoność czasową T(n) ${\displaystyle \in }$ O(n²).

Przypadek średni

Przy założeniu, że wszystkie możliwe wartości tablicy A występują z jednakowym prawdopodobieństwem, można dowieść, że oczekiwana liczba elementów A[1..i] większych od wstawianego klucza wynosi i/2. W tym wypadku podstawienie δ(i) = i/2 daje podobnie jak w przypadku pesymistycznym złożoność T(n) ${\displaystyle \in }$ O(n²).

Poprawność

Prawidłowość algorytmu sortowania przez wstawianie można dowieść, udowodniając poniższe twierdzenie:

w i-tym wykonaniu pętli for tablica A[1..i-1] składa się z posortowanych elementów znajdujących się w pierwotnej tablicy na pozycjach [1..i-1].

Dowód:

W pierwszej iteracji, dla i=1 zdanie jest prawdziwe (rozważamy posortowany ciąg A[1..1]).

W l-tej iteracji, jeżeli elementy A[1..l-2] są posortowane, to nowy klucz zostanie wstawiony na pozycję, w której nie będzie tworzył inwersji z żadnym z elementów w zbiorze do którego zostanie dołączony, a więc zbiór A[1..l-1] będzie posortowany.

W ostatniej iteracji pętli ostatni wolny klucz zostaje wstawiony w posortowany ciąg A[1..n-2] w wyniku czego powstaje posortowana tablica A[1..n-1]

Bezpośredni wniosek z powyższego twierdzenia: algorytm sortowania przez wstawianie dla każdej tablicy A dokona jej prawidłowego posortowania.

Przykłady implementacji

• Zobacz przykładowe implementacje sortowania przez wstawianie na Wikibooks

Zobacz też

• Sortowanie Shella
• Sortowanie przez wybieranie

Przypisy

Bibliografia

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Wprowadzenie do algorytmów. WNT, 2007.

Linki zewnętrzne

• Algorytm przedstawiony z wykorzystaniem rumuńskiego tańca