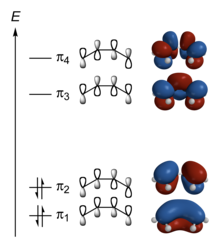Sprzężone wiązania wielokrotne

Czerwonym kolorem wyróżniono tę część cząsteczki, w której elektrony z atomowych orbitali p węgla można uważać za jednowymiarowy gaz elektronowy. Są one w dużym stopniu swobodne, co przypomina wiązanie metaliczne. Dla każdego z elektronów znajdujących się w jednowymiarowej studni potencjału można obliczyć wartość energii wzbudzenia, np. wskutek absorpcji światła[1][2]. Pozwala to wyjaśnić np. barwę marchwi (maksima absorpcji: 451 i 477 nm[3]).
Sprzężone wiązania wielokrotne (układ sprzężonych wiązań wielokrotnych) – określenie dotyczące budowy cząsteczek związków organicznych, w których poza wiązaniami sigma (σ) formalnie istnieją co najmniej dwa wiązania wielokrotne pi (п) lub delta (δ), rozdzielone jednym wiązaniem pojedynczym. W takiej sytuacji energetycznie korzystna jest dalsza delokalizacja elektronów z atomowych orbitali p lub d, leżących prostopadle do płaszczyzny wiązań sigma. Zdelokalizowane elektrony walencyjne zajmują wielocentrowe orbitale molekularne (cząsteczkowe). W niektórych przypadkach są traktowane jak elektrony swobodne w jednowymiarowej studni potencjału – rodzaj gazu elektronowego[1][2][4][5].
Popularnymi przykładami cząsteczek z układem sprzężonych wiązań podwójnych C=C są związki aromatyczne oraz niektóre dieny (dwa sprzężone wiązania C=C, np. 1,3-butadien) i polieny. Sprzężenie wielu wiązań wielokrotnych wyjaśnia przewodnictwo polimerów („metaliczność” wiązania między niemetalami) oraz barwę licznych pigmentów. Łańcuch polienowy jest chromoforem pochłaniającym promieniowanie w zakresie widzialnym. Ten efekt leży u podstaw widzenia barw (widzenie fotopowe). Zawdzięczają mu barwę np. liczne karoteny i chlorofile[1][2][4][5].
Układy wielokrotnych wiązań sprzężonych występują również w cząsteczkach nitryli (np. sprzężenie C=C z C≡N w cząsteczkach akrylonitrylu lub benzonitrylu) lub nienasyconych ketonów (np. sprzężenie C=C z C=O w cząsteczce aldehydu cynamonowego)[1][2][4][5].
Budowa cząsteczek i ich modele
Cząsteczki związków chemicznych są strukturami złożonymi z pewnej ilości rdzeni atomowych (jądra atomów i elektrony powłok wewnętrznych), praktycznie nieulegających zmianom w warunkach typowych dla reakcji chemicznych, oraz odpowiedniej liczby ruchliwych elektronów walencyjnych, zajmujących przestrzeń wokół rdzeni.
Stosowanie w takich złożonych układach fizycznych klasycznej definicji zlokalizowanego wiązania chemicznego prowadzi do uproszczonych modeli cząsteczek, nie zawsze wyjaśniających rzeczywiste chemiczne i fizyczne właściwości związków. Odzwierciedleniem takich modeli są np. klasyczne wzory strukturalne, w których kreska łącząca symbole pierwiastków odpowiada zlokalizowanej wiążącej parze elektronowej. W przypadkach stwierdzenia delokalizacji tych elektronów są stosowane strzałki, określające kierunki przesunięć. Wprowadzono też pojęcia ładunków umownych i ułamkowych krotności wiązania.

Modele cząsteczek wynikające z założeń mechaniki kwantowej opierają się na pojęciu prawdopodobieństwa określonych zdarzeń. Na podstawie równania Schrödingera określa się energie elektronów oraz granice obszarów, w przestrzeni otaczającej jądra atomów, w których się poruszają. Orbitale atomowe, np. s, p, d, f, wskazują obszary, w których elektron znajduje się najczęściej (prawdopodobieństwo np. > 90%). Analogiczne funkcje falowe Ψ elektronów w cząsteczkach związków chemicznych oblicza się metodami przybliżonymi. Stosuje się np.[1]:
- metodę liniowych kombinacji atomowych funkcji Ψ, pozwalających opisać orbitale molekularne (metoda orbitali molekularnych MO; F. Hund i Robert S. Mulliken, Nagroda Nobla w dziedzinie chemii, 1966)
- metodę liniowych kombinacji funkcji Ψ tzw. granicznych, hipotetycznych struktur rezonansowych (struktur kanonicznych), zawierających wyłącznie wiązania zlokalizowane (metoda wiązań walencyjnych, valence bond VB; J.C. Slater 1931, L. Pauling 1933; Nagroda Nobla w dziedzinie chemii, 1954).
W czasie obliczeń poszukuje się takich wartości wag, przypisywanych poszczególnym funkcjom Ψ, które zapewniają osiągnięcie najmniejszej energii wewnętrznej opisywanego układu (stan podstawowy cząsteczki)[1][2].
Najdalej idącą próbą opisu struktury cząsteczek z elektronami zdelokalizowanymi jest wykorzystanie rozwiązań równania Schrödingera dla elektronu swobodnego w jednowymiarowej studni potencjału (zobacz: cząstka w studni potencjału)[1][2].
Cząsteczka benzenu

Cząsteczka benzenu jest układem złożonym z sześciu zrębów atomowych węgla, sześciu protonów (jądra atomowe wodoru) i 30 elektronów walencyjnych. Spośród tych elektronów 24 tworzą zlokalizowane wiązania sigma, ułożone względem siebie pod kątem 120°. Jest to zgodne z zasadami hybrydyzacji sp2 i gwarantuje najmniejsze wzajemne boczne nakładanie się. Prostopadle do płaszczyzny, na której leży tak skonstruowany pierścieniowy zrąb molekularny, mogą ustawić się atomowe orbitale pozostałych 6 elektronów p (sekstet). Takie równoległe orbitale nakładają się bocznie (wiązanie πp–p) w dużej odległości od płaszczyzny wiązań sigma, czyli w obszarze, gdzie prawdopodobieństwo znalezienia elektronów jest bardzo małe. Takie słabe wiązanie nie wyjaśnia trwałości cząsteczki benzenu.
Zgodnie z propozycją Kekulégo powstają struktury z trzema wiązaniami podwójnymi i trzema pojedynczymi. Brak zgodności tej hipotezy z doświadczalnie stwierdzoną równocennością wszystkich wiązań pierścienia próbowano wyjaśnić efektem rezonansu.
W czasie obliczeń, wykonywanych zgodnie z zasadami mechaniki kwantowej metodą struktur walencyjnych (VB), struktury Kekulégo są brane pod uwagę jako struktury kanoniczne, czyli hipotetyczne struktury graniczne. Uwzględniane są również inne hipotetyczne układy z wiązaniami zlokalizowanymi, np. trzy struktury Dewara[a].
Wynikiem obliczeń wykonywanych metodą orbitali molekularnych (MO) jest sześć zdelokalizowanych orbitali cząsteczkowych – 3 wiążące i 3 niewiążące. W cząsteczce benzenu w stanie podstawowym, elektrony sekstetu obsadzają trzy orbitale wiążące (trzy pary elektronowe w dwóch torusach – nad i pod płaszczyzną wiązań sigma). Orbitale o wyższych energiach, łącznie również tworzące torus, są zajmowane po wzbudzeniu cząsteczki (np. absorpcji kwantu promieniowania)[4].
Tak zbudowany układ ma mniejszą energię wewnętrzną niż hipotetyczny cykloheksatrien. Różnica między energią cząsteczki benzenu z elektronami zdelokalizowanymi (struktura rzeczywista w stanie podstawowym) i zlokalizowanymi (struktura Kekulégo), zwana energią stabilizacji aromatycznej, energią stabilizacji przez sprzężenie albo energią rezonansu wynosi około 40 kcal/mol[4]. Porównując np. dwie wartości energii[5]:
- suma energii wiązań (E) w strukturze Kekulégo:
- 3 × EC–C + 3 × EC=C + 6 × EC–H = 3 × 81 + 3 × 146,5 + 6 × 98,5 = 1273,5 kcal/mol
- doświadczalnie oznaczone ciepło tworzenia benzenu: 1310 kcal/mol
otrzymuje się wartość energii stabilizacji przez sprzężenie
- 1310 − 1273,5 = 36,9 kcal/mol
Podobną wartość energii sprzężenia uzyskuje się porównując zmierzone i obliczone dla struktury Kekulego wartości energii uwodornienia. W tabeli zestawiono dane dotyczące benzenu i etylobenzenu z analogicznymi wynikami, charakteryzującymi energię sprzężenia w cząsteczkach z dwoma sprzężonymi wiązaniami podwójnymi.
| Związek chemiczny | Ciepło zmierzone | Ciepło obliczone | Energia sprzężenia |
| benzen | 49,8 | 85,8 | 36 |
| etylobenzen | 48,9 | 84,1 | 35,2 |
| cykloheksadien | 55,4 | 57,2 | 1,8 |
| cyklopentadien | 50,9 | 53,8 | 2,9 |
| 1,3-butadien | 57,1 | 60,6 | 3,5 |
Cząsteczka 1,3-butadienu

W cząsteczce 1,3-butadienu, zbudowanej z czterech atomów węgla i sześciu atomów wodoru, powstaje zrąb molekularny, powiązany dziewięcioma wiązaniami sigma. Ponieważ te wiązania powstają w efekcie nałożenia orbitali s wodoru i orbitali sp2 węgla, zrąb leży na płaszczyźnie, a kąty między wiązaniami wynoszą 120°.
Pozostałe elektrony walencyjne, to elektrony p węgla (po jednym od każdego z atomów C), o orbitach atomowych ustawionych prostopadle do płaszczyzny wiązań σ. Liniowa kombinacja tych funkcji falowych (metoda LCAO) prowadzi do wyznaczenia czterech orbitali molekularnych:
- π1 – wiążąca para elektronowa, elektrony zdelokalizowane w zakresie od C1 do C4 (podwyższa energię wszystkich wiązań)
- π2 – wiążąca para elektronowa; elektrony zdelokalizowane w zakresach od C1–C2 i C3–C4 (odpowiednik klasycznego zapisu położenia wiązań zlokalizowanych)
- π3 – para elektronowa wiążąca tylko dla C2 i C3
- π4 – para elektronowa, która nie podwyższa energii żadnego z wiązań C–C.
Elektrony atomowe p zajmują więc w stanie podstawowym cząsteczki butadienu orbitale molekularne π1 i π2. Całkowity rozkład ładunków w tym stanie wyraża suma ładunków elektronów z obu orbitali. Suma wskazuje, że energia wiązania C2–C3 jest większa niż energia odpowiedniego wiązania σ (przewidywanego zgodnie z zapisem C1=C2–C3=C4).
α,β-Nienasycone aldehydy i ketony
W licznych α,β-nienasyconych aldehydach i ketonach (np. aldehyd krotonowy, aldehyd cynamonowy lub tlenek mezytylu) występuje sprzężenie między wiązaniami C=C i C=O. Jest to przyczyną charakterystycznych zmian właściwości fizycznych. Zaobserwowano, że wskutek tego sprzężenia refrakcja molowa takich związków jest większa od refrakcji obliczonych z refrakcji wiązań (brak addytywności, zjawisko „egzaltacji”)[b][5].
Występowanie sprzężenia decyduje też o przebiegu niektórych reakcji chemicznych, np. reakcji uwodornienia. Stwierdzono, że układ sprzężony C=C-C=O ulega uwodornieniu trudniej, niż izolowane wiązanie C=C. W przypadkach, gdy w cząsteczce występuje nie sprzężone z tym układem, dodatkowe wiązanie C=C, ulega ono uwodornieniu w pierwszej kolejności[5][c].
Elektrony п polienów w studni potencjału

Zdelokalizowane elektrony walencyjne π łańcucha polienowego bywają traktowane jak gaz elektronowy (elektrony swobodne), znajdujący się w jednowymiarowej „studni potencjału” (zobacz też: cząstka w studni potencjału). Uznaje się, że granicami studni są końce łańcucha, stanowiące dla elektronów nieskończenie wysoką barierę potencjału. Elektron może przemieszczać się tylko wzdłuż łańcucha, powyżej i poniżej niego. Zaniedbuje się zmiany energii, zależne od chwilowej odległości od kolejnych jąder atomów węgla (tzw. elektron swobodny nie ma energii potencjalnej). Rozwiązując równanie Schrödingera dla każdego z tak opisanych elektronów π otrzymuje się zależność[1][2]:
gdzie: n – liczba kwantowa (kolejne liczby naturalne), h – stała Plancka, m – masa elektronu, l – szerokość studni (długość łańcucha polienowego).
W stanie podstawowym elektrony wypełniają najniższe poziomy (najmniejsze wartości n). Najłatwiejsze wzbudzenie cząsteczki polega na pochłonięciu kwantu (hc/λ), którego wielkość jest równa różnicy między energią elektronu na najwyższym zajętym poziomie i najbliższym poziomie wolnym. W czasie badań absorpcji światła oznacza to absorpcję w najbardziej długofalowym zakresie widma. Długość fali absorbowanego wówczas światła jest oznaczana symbolem λmaks [μm][1][2].
Według W. Kuhna (1948) wartość λmaks [nm] można obliczyć z wzoru[6]:
Wykonanie stosunkowo prostych obliczeń pozwala więc przewidywać barwę związku na podstawie informacji o długości łańcucha polienowego (liczba atomów węgla × średnia długość wiązania). W tabeli zestawiono dla przykładu wartości zmierzone i obliczone dla kilku polienów[1].
| Związek chemiczny | Liczba wiązań podwójnych | λ obliczone | λ zmierzone |
| butadien | 2 | 233 | 217 |
| heksatrien | 3 | 282 | 258 |
| oktatetraen | 4 | 320 | 302 |
| dehydro-β-karoten | 12 | 461 | 475 |
| dehydrolikopen | 15 | 486 | 504 |
Wpływ na właściwości elektryczne i magnetyczne
Z delokalizacją i swobodą przemieszczania się elektronów π w układzie sprzężonych wiązań wielokrotnych wiąże się wysoka i silnie anizotropowa polaryzowalność cząsteczek, a także silnie anizotropowa podatność magnetyczna[7].
Uwagi
- ↑ Pojęcie „struktura Dewara” oznacza tu jedną z hipotetycznych struktur granicznych. Zobacz też: benzen Dewara.
- ↑ Zjawisko egzaltacji występuje w przypadku wielu związków z układami wiązań sprzężonych podwójnych i potrójnych. Było wykorzystywane przy rozwiązywaniu zagadnień strukturalnych (wykrywanie sprzężeń). Egzaltacja występuje w przypadku polienów o łańcuchach otwartych. W przypadku benzenu obserwowane jest zmniejszenie refrakcji wskutek sprzężenia [Nenitescu, s. 117–120]
- ↑ Sprzężenie wiązań wielokrotnych decyduje też o przebiegu reakcji przyłączania do układu C=C–C≡N, np. przyłączania amin, amoniaku lub alkoholi do akrylonitrylu [Sokołowski, Kupryszewski, s. 351–352]
Zobacz też
- Metoda wariacyjna
- Metoda Ritza
Przypisy
- ↑ a b c d e f g h i j k Heinz A. Staab: Wstęp do teoretycznej chemii organicznej. Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1966, s. 75–...–124–...
- ↑ a b c d e f g h Stanisław Bursa: Chemia fizyczna, rozdz. Przykłady zastosowań równania Schrödingera; Widma cząsteczkowe; Fotochemia. Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1979, s. 46–64, 116–154. ISBN 83-01-00152-6.
- ↑ Uniwersytet Gdański: Wyodrębnienie i właściwości beta karotenu. [w:] Materiały dydaktyczne; pr_dyp_cw_7 (pdf) [on-line]. ppc.uniw.gda.pl. [dostęp 2011-06-15]. (pol.).
- ↑ a b c d e Janusz Sokołowski: Teoretyczne podstawy chemii organicznej. Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1972, s. 46–66, 346–354.Sprawdź autora:1.
- ↑ a b c d e f g N.C. Nenitescu: Chemia organiczna, tom I. Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1967, s. 70–78, 298–310.
- ↑ Hans Kuhn. A Quantum-Mechanical Theory of Light Absorption of Organic Dyes and Similar Compounds. „Journal of Chemical Physics”. 17 (12), s. 1210, 1949. (ang.).
- ↑ Hermann Haken, Hans Christoph Wolf: Fizyka molekularna z elementami chemii kwantowej. Warszawa: PWN, 1998, s. 323. ISBN 83-01-12630-2.
Media użyte na tej stronie
Autor:
- Pisystem_Benzol.svg: Gmeyer
- derivative work: Joanna Kośmider (talk)
Pi-Orbitals of Benzen sorted by energy
Autor: An elite, Licencja: CC BY-SA 3.0
Benzene molecule. Hydrogen atoms are shown, and π bonds are shown as delocalized.
Benzen; 5 struktur kanonicznych
Autor: Papa November, Licencja: CC BY-SA 3.0
Initial wavefunctions for the lowest four quantum states of a particle trapped in an infinitely deep quantum well. The spatial position is shown along the horizontal axis. The red regions represent barriers with an infinitely large potential, while the area between the barriers represents a well with zero potential.
The wavefunction for each state is given by
Autor: Xavier Andrade, Licencja: CC-BY-SA-3.0
Ground state density of Benzene (C6H6), isosurface rho=0.1 [au]. Density calculated by octopus, image created using en:OpenDx.
beta-carotene with conjugation highlighted
Energy level diagram of the π molecular orbitals of butadiene (forced to adopt a planar cis conformation, for the purposes of discussing cycloadditions).
Structures calculated and images produced using HF/6-31G* in Spartan '04 Student Edition and ChemDraw Ultra 11.0.
Energy of orbitals:
π4: +7.71713 eV
π3: +3.16186 eV (LUMO)
π2: −8.66624 eV (HOMO)
Structure of cinnamaldehyde