Stożek świetlny

Stożek świetlny (stożek zerowy) danego punktu czasoprzestrzeni – zbiór punktów czasoprzestrzeni, których odległość czasoprzestrzenna (interwał) od tego punktu wynosi zero^[1][2] (stąd nazwa „stożek zerowy”), co oznacza, że zdarzenie czasoprzestrzenne zachodzące w danym punkcie czasoprzestrzeni można połączyć ze zdarzeniem zachodzącym w dowolnym punkcie jego stożka świetlnego sygnałem przesłanym z prędkością graniczną, równą prędkości światła w próżni^[2][3] (stąd nazwa „stożek świetlny”).

Z punktu widzenia obserwatora w trójwymiarowej przestrzeni fizycznej, stożek świetlny to sfera (dwuwymiarowa), o środku w danym punkcie, rozszerzająca się z prędkością światła, stanowiąca czoło kulistej fali świetlnej, wysłanej z danego punktu (część przyszłościowa stożka, tzw. stożek przyszłości) lub kurcząca się z prędkością światła, stanowiąca czoło kulistej fali świetlnej, zbiegającej się w danym punkcie (część przeszłościowa stożka, tzw. stożek przeszłości)^[1].

Zbiór punktów, tworzących tę sferę w kolejnych momentach czasu (lub, mówiąc inaczej, zbiór punktów wszystkich dwuwymiarowych, momentalnych sfer) stanowi trójwymiarową (dwa wymiary przestrzenne i czas) hiperpowierzchnię zanurzoną w czterowymiarowej czasoprzestrzeni, spełniającą równanie powierzchni stożka obrotowego, o wierzchołku w danym punkcie^[4][5].

Stożek świetlny można przyporządkować każdemu punktowi czasoprzestrzeni.

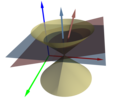
Model trójwymiarowy

W modelu trójwymiarowym, wymiar czasu reprezentowany jest przez jeden z wymiarów przestrzennych. Oś stożka, przebiegająca w rzeczywistości w wymiarze czasu, reprezentowana jest przez oś przebiegającą w tym wymiarze przestrzennym.

Dwuwymiarowe sfery, w kolejnych momentach czasu, są reprezentowane przez jednowymiarowe okręgi, o wzrastającym promieniu i środkach w kolejnych punktach osi stożka^[6]. Zbiór punktów tych okręgów stanowi dwuwymiarową powierzchnię stożkową, zanurzoną w trójwymiarowej przestrzeni.

Tworzącymi stożka świetlnego są linie świata cząstek poruszających się z prędkością graniczną – luksonów (np. fotonów)^[6][7]. Jeśli czas i przestrzeń wyrażone są w tych samych jednostkach, to nachylenie tworzących stożka do osi układu współrzędnych wynosi połowę kąta pomiędzy osiami (linia świata luksonu jest dwusieczną tego kąta^[6][8].

Podział czasoprzestrzeni

Stożek świetlny danego punktu czasoprzestrzeni dzieli czasoprzestrzeń na pięć obszarów, ze względu na związek przyczynowo-skutkowy między zdarzeniem zachodzącym w danym punkcie a zdarzeniami zachodzącymi w tych obszarach^{[2][9][10][11]}.

1) Obszar zdarzeń wcześniejszych od danego zdarzenia, które mogą wpłynąć na nie za pośrednictwem cząstek o niezerowej masie niezmienniczej – tardionów (każde takie zdarzenie dzieli od danego zdarzenia przedział typu czasowego); wnętrze stożka przeszłości.

2) Obszar zdarzeń wcześniejszych od danego zdarzenia, które mogą wpłynąć na nie jedynie za pośrednictwem cząstek o zerowej masie niezmienniczej – luksonów (każde takie zdarzenie dzieli od danego zdarzenia przedział zerowy); powierzchnia stożka przeszłości.

Obszar 1) i 2) razem to absolutna przeszłość danego zdarzenia (obszar jego przyczyn).

3) Obszar zdarzeń późniejszych od danego zdarzenia, na które może ono wpłynąć jedynie za pośrednictwem luksonów (każde takie zdarzenie dzieli od danego zdarzenia przedział zerowy); powierzchnia stożka przyszłości.

4) Obszar zdarzeń późniejszych od danego zdarzenia, na które może ono wpłynąć za pośrednictwem tardionów (każde takie zdarzenie dzieli od danego zdarzenia przedział typu czasowego); wnętrze stożka przyszłości.

Obszar 3) i 4) razem to absolutna przyszłość danego zdarzenia (obszar jego skutków).

5) Obszar zdarzeń wcześniejszych lub późniejszych od danego zdarzenia (lub z nim równoczesnych), które nie mogą na nie wpłynąć, i na które nie może ono wpłynąć w żaden sposób (każde takie zdarzenie dzieli od danego zdarzenia przedział typu przestrzennego); zewnętrze stożka.

Obszar 5) to obszar zdarzeń wobec danego zdarzenia „obojętnych”, „niedostępnych”^[12], „absolutnie oddalonych”^[2], leżących „gdzie indziej”^[10], „quasiteraźniejszość”^[13].

Ponieważ przedział czasoprzestrzenny jest niezmiennikiem, ten podział czasoprzestrzeni nie zależy od wyboru układu odniesienia^[9]. Natomiast obszar zewnętrza stożka w różnych układach odniesienia jest różnie podzielony na hiperpłaszczyznę względnej teraźniejszości danego zdarzenia oraz obszary jego względnej przeszłości i względnej przyszłości.

Nieinercjalne układy odniesienia

Położenie i kształt stożka świetlnego są jednakowe we wszystkich inercjalnych układach odniesienia^[4][9], ale zmieniają się w układach nieinercjalnych, w szczególności pod wpływem pola grawitacyjnego^[14].

Stożek świetlny w kulturze

Wizerunek trójwymiarowego modelu stożka świetlnego był symbolem Światowego Roku Fizyki.

Przypisy

Bibliografia

• Zdzisław Augustynek: Przeszłość, teraźniejszość, przyszłość. PWN, 1979.
• Bożena Muchotrzeb: Jak płynie czas, w: Czas. WSiP, 1983.
• M. Sawicki: Elementy teorii względności. Zajęcia fakultatywne w grupie matematyczno-fizycznej. WSiP, 1975.
• A. Szymacha: Szczególna teoria względności. Alfa, 1985.
• E. F. Taylor, J. A. Wheeler: Fizyka czasoprzestrzeni. PWN, 1975.
• W. A. Ugarow: Szczególna teoria względności. PWN, 1985.