Symulacja komputerowa
Symulacja komputerowa – program komputerowy symulujący wybrane zjawisko fizyczne lub społeczne, najczęściej implementujący jego model matematyczny. Techniki symulacyjne są szczególnie przydatne tam, gdzie analityczne wyznaczenie rozwiązania byłoby zbyt pracochłonne, a niekiedy nawet niemożliwe, co często ma miejsce w systemach złożonych.
Rodzaje symulacji komputerowych
Symulacje komputerowe można podzielić ze względu na:
- przewidywalność zdarzeń
- stochastyczne – korzystają z generatora liczb pseudolosowych lub (bardzo rzadko) losowych (szczególnie popularna jest metoda Monte Carlo).
- deterministyczne – wynik jest powtarzalny i zależy tylko od danych wejściowych i ewentualnych interakcji ze światem zewnętrznym.
- rozmyte
- sposób upływu czasu
- z czasem ciągłym[1] – czas zwiększa się stałymi przyrostami, jak w symulacji z czasem dyskretnym, lecz wartości próbek sygnałów są interpolowane dla chwil pośrednich pomiędzy momentami odczytu.
- z czasem dyskretnym – czas zwiększa się stałymi przyrostami, a krok czasowy dobiera się optymalnie ze względu na zasobożerność systemu, jego wydajność i charakter symulowanego obiektu i/lub zjawiska (mikrosekundy w obwodach elektrycznych i miliony lat przy symulacji ewolucji gwiazd).
- symulacja zdarzeń dyskretnych – czas zwiększa się skokowo, ale jego przyrosty są zmienne (ważniejsza jest tu sekwencja zdarzeń niż rzeczywisty lub wirtualny upływ czasu).
- formę danych wyjściowych
- statyczne – wynikiem jest zbiór danych, statyczny obraz itp.
- dynamiczne – wynikiem jest proces przebiegający w czasie np. animacja.
- interaktywne – reagują na sygnały ze świata zewnętrznego np. operatora.
- nieinteraktywne
- liczbę użytych komputerów
- lokalne – przetwarzanie odbywa się na pojedynczym komputerze.
- rozproszone – przetwarzanie odbywa się w wielu komputerach połączonych w sieci lokalnej (LAN) lub zewnętrznej np. Internet.
- liczbę zmiennych niezależnych
- o parametrach skupionych
- o parametrach rozłożonych
Narzędzia stosowane do symulacji
Program symulacyjny może być napisany w dowolnym języku programowania. W ograniczonym zakresie można do symulacji wykorzystać również arkusz kalkulacyjny. Zostały jednak stworzone specjalne narzędzia przeznaczone do wykonywania symulacji komputerowych. Obecnie stosowane są np.:
- język programowania GPSS
- Crystal Ball
- @Risk
- Arena
- SciLab
- FlexSim
Jednym z nietypowych dostępnych języków programowania jest ModSim oparty na Microsoft Visual C++ w wersji 1.5, choć programuje się w nim w języku podobnym do Pascala (za pomocą translatora jest zamieniany na C++). Posiada on mechanizmy do przeprowadzania zaawansowanych symulacji m.in. monitory i generatory liczb losowych. Możliwe jest też wizualizowanie w czasie rzeczywistym zachodzących procesów za pomocą np. wektorowych funkcji rysujących.
Najczęściej jednak używanym językiem programowania w symulacji komputerowej jest Python. Jest on darmowy, ma intuicyjną składnię, dla tego języka opracowania szereg bibliotek o otwartym kodzie, łatwo więc znaleźć przykłady użycia.
Wybrane zastosowania symulacji
- symulatory statków powietrznych, okrętów podwodnych, czołgów itp.
- w ekonomii i biznesie
- systemy kolejkowe
- zarządzanie zapasami
- wycena instrumentów pochodnych (np. opcji)
- ocena projektów inwestycyjnych (m.in. VaR)
- w naukach społecznych
- Dynamiczna teoria wpływu społecznego Nowaka-Latane
- prognozowanie podziału miejsc w parlamencie
- dynamika populacji
- nauki przyrodnicze
- meteorologia – prognozy pogody
- analiza rozprzestrzeniania się zanieczyszczeń (np. dyspersji odorantów)
- w naukach inżynieryjnych
- budownictwo – wytrzymałość konstrukcji
- lotnictwo – wytrzymałość konstrukcji
- elektronika – analiza obwodów elektrycznych
- matematyka
- numeryczne wyznaczanie rozwiązań równań różniczkowych
- symulacyjne wyznaczanie dystrybuant funkcji, które nie dają się całkować (np. rozkładu normalnego)
- komputerowe gry symulacyjne
Przykład zastosowania
Obiektem symulacji jest sklep, którego dochody (zmienna wyjściowa) są uzależnione od wielu czynników (zmiennych wejściowych), np. liczba klientów odwiedzających sklep, cena podobnych towarów sprzedawanych u konkurencji, poziom sprzedaży w danym miesiącu. Przyjmuje się, że każdy z tych czynników jest zmienną losową o pewnym rozkładzie, np. normalnym.
Celem symulacji komputerowej jest przeprowadzenie kilkuset (albo kilku tysięcy albo kilkuset tysięcy) eksperymentów polegających na wylosowaniu konkretnych wartości poszczególnych zmiennych (czyli np. w jednej symulacji wylosowano następujące wartości: liczba klientów = 125, cena u konkurencji = 43 zł, poziom sprzedaży = 27 sztuk) i sprawdzeniu jaki dochód zostanie osiągnięty przy takich założeniach.
Po wielokrotnym przeprowadzeniu symulacji (czyli losując różne wartości zmiennych) możemy stwierdzić, jak wygląda rozkład dochodu sklepu. Na tej podstawie można np. wyznaczyć wartość oczekiwaną zysku, prawdopodobieństwo straty i inne interesujące z biznesowego punktu widzenia wielkości.
Problemy
Ten przykład ukazuje najistotniejsze problemy symulacji:
- złożoność zaprojektowanej symulacji (ile i jakie czynniki będą uwzględnione oraz w jaki sposób)
- adekwatność osiągniętych wyników
Złożoność zwykle jest związana ze stopniem skomplikowania projektu, co przekłada się w prostej linii na koszty oraz jakość wyników.
Natomiast adekwatność wyników do np. danych zarejestrowanych w rzeczywistych eksperymentach, jest powodem wielu dyskusji np. naukowych. Jeśli osiągnięte wyniki dalece odbiegają od zaobserwowanych faktów, kwestionowana jest zasadność tego typu symulacji.
Przypisy
- ↑ Rzeczywisty czas ciągły możliwy jest do uzyskania jedynie w symulatorach analogowych, zob. komputer analogowy.
Zobacz też
Linki zewnętrzne
- Eric Winsberg, Computer Simulations in Science, [w:] Stanford Encyclopedia of Philosophy [online], CSLI, Stanford University, 23 kwietnia 2015, ISSN 1095-5054 [dostęp 2018-01-16] (ang.). (Symulacje komputerowe w nauce)
Media użyte na tej stronie
Autor:
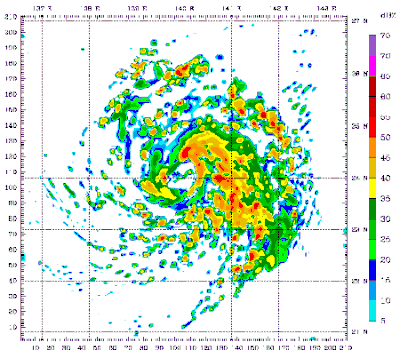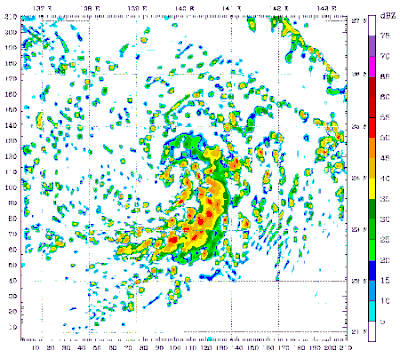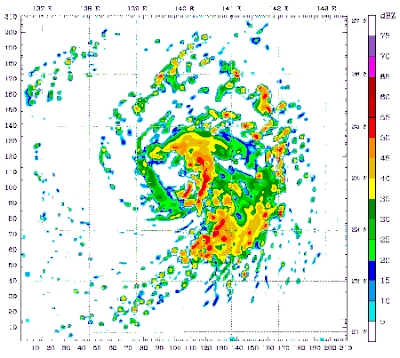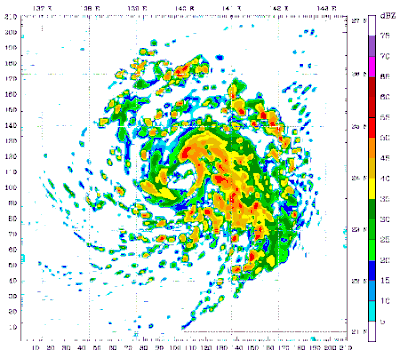
- Typhoon_Mawar_2005_computer_simulation.gif: Atmoz
- derivative work: Atmoz (talk)
A 48 hour simulation of Typhoon Mawar using the Weather Research and Forecasting model. At this time, Mawar was at approximately 24N 140E and moving slowly to the north. Initial conditions and boundary conditions are from the 1 degree FNL reanalysis (approximately 110 kilometers, 68 miles). The simulation runs from 22 August 2005 00:00 Zulu to 24 August 2005 00:00 Zulu. The model has 3.3 kilometre (2.1 mile) grid point spacing, and utilizes vortex following which is why the typhoon remains in the middle of the frame. Approximately the first 24 hours (frames) show the model "spinning up"— which is the amount of time needed for the model physics to reach equilibrium with the applied boundary conditions. After the initial round of convection in the first couple frames, gravity waves can be seen propagating outward from the center of convection, especially in the northwest quadrant of the storm system. The final 24 hours (frames) represent a high resolution simulation of the actual typhoon. The reds and oranges represent high rainfall rates, blues and greens light rainfall, and the white are regions of no rainfall.
