Technika kolorowania dziedziny

Ten artykuł od 2017-03 wymaga zweryfikowania podanych informacji. Należy podać wiarygodne źródła, najlepiej w formie przypisów bibliograficznych. Część lub nawet wszystkie informacje w artykule mogą być nieprawdziwe. Jako pozbawione źródeł mogą zostać zakwestionowane i usunięte. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Wykres funkcji ${\displaystyle \sin(1/z)}$ uzyskany sposobem pierwszym

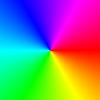
Technika kolorowania dziedziny – sposób prezentacji wykresu funkcji zmiennej zespolonej. Polega on na przypisaniu kolorów z koła barw do płaszczyzny zespolonej. Możliwe są różne przekształcenia lecz w praktyce stosuje się dwa:

1. Środek płaszczyzny zespolonej jest biały, liczba 1 jest czerwona, liczba −1 jest błękitno turkusowa a punkt w nieskończoności jest czarny.
2. Środek płaszczyzny zespolonej jest czarny, liczba 1 jest błękitno turkusowa, liczba −1 jest czerwona a punkt w nieskończoności jest biały.

W obu przypadkach najbardziej nasycone kolory znajdują się na okręgu jednostkowym. Bardziej precyzyjnie, argument liczby zespolonej utożsamia się z odcieniem H natomiast moduł z jasnością L w przestrzeni kolorów HSL. Dla tak uzyskanej pary (H, L) ostatni trzeci parametr S (nasycenie) ustawia się na wartość maksymalną.

${\displaystyle f(z)=z}$

Kompletny wykres

Moduł

Argument

Część rzeczywista

Część urojona

Wykres funkcji zespolonej odwzorowany techniką kolorowania dziedziny sposobem drugim

Linki zewnętrzne

• Metoda koła barw. wmi.math.u-szeged.hu. [zarchiwizowane z tego adresu (2007-01-01)]. (ang.)
• Kolorowe wykresy funkcji zmiennej zespolonej. w.american.edu. [zarchiwizowane z tego adresu (2017-03-17)]. (ang.)