Teoria grawitacji Le Sage’a

Ten artykuł od 2016-04 zawiera treści, przy których brakuje odnośników do źródeł. Należy dodać przypisy do treści niemających odnośników do wiarygodnych źródeł. (Dodanie listy źródeł bibliograficznych lub linków zewnętrznych nie jest wystarczające). Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Teoria grawitacji Le Sage'a jest kinetyczną teorią grawitacji, zaproponowaną pierwotnie w 1690 roku przez Nicolasa Fatio de Duilliera, a następnie w 1748 przez Georgesa-Louisa Le Sage. Stanowiła ona propozycję mechanicznego wyjaśnienia siły grawitacji Newtona za pomocą strumieni drobnych, niewidocznych cząstek (które Le Sage nazwał korpuskułami ultra-tymczasowymi), bombardującymi wszystkie ciała materialne ze wszystkich kierunków. Zgodnie z tym modelem, dowolne dwa ciała materialne częściowo się wzajemnie ekranują przed nadbiegającymi korpuskułami, co skutkuje ogólnym niezbalansowaniem ciśnienia na nie wywieranego i tendencjami do wzajemnego przybliżania się. Takie mechaniczne wyjaśnienie grawitacji nigdy nie zyskało powszechnej akceptacji, chociaż było od czasu do czasu studiowane przez fizyków aż do początków XX wieku, kiedy to powszechnie uznano je za niezbicie zdyskredytowane.

Podstawy teorii

P1: Pojedyncze ciało.
Brak wypadkowej siły.

Teoria zakłada, że siła grawitacji jest wynikiem działania malutkich cząstek (korpuskuł), poruszających się szybko we wszystkich kierunkach i wypełniających Wszechświat. Zakłada się, że natężenie strumienia cząstek jest takie samo we wszystkich kierunkach, tak więc izolowany obiekt A jest uderzany równomiernie ze wszystkich stron, co skutkuje jedynie dośrodkowym ciśnieniem, lecz nie ukierunkowaną siłą wypadkową (P1).

P2: Dwa ciała „przyciągają się” wzajemnie.

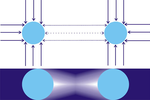
W obecności drugiego ciała B, część cząstek, która w przeciwnym razie uderzałaby ciało A z kierunku, w którym znajduje się B, zostaje przechwycona, zatem B działa jak ekran. Ze strony ciała B w A uderza mniej cząstek, niż z przeciwnej strony. Można powiedzieć, że A i B wzajemnie się „ocieniają”, czego wynikiem jest popychanie ich ku sobie przez niezrównoważenie sił (P2). Zatem widoczne przyciąganie pomiędzy ciałami jest w istocie zmniejszonym pchaniem z kierunku drugiego ciała, teoria ta jest więc czasem nazywana grawitacją pchaną lub grawitacją cienia, choć szerzej znana nazwa to grawitacja Le Sage'a.

Natura zderzeń

P3: Przeciwne strumienie.

Jeżeli zderzenia grawitacyjnych cząstek z ciałem A są w pełni sprężyste, intensywność odbitych cząstek byłaby tak samo silna, jak nadbiegających, nie powstałaby więc żadna ukierunkowana wypadkowa siła. To samo byłoby prawdziwe po wprowadzeniu ciała B, gdzie B działałoby jak osłona dla cząstek biegnących ku A. Cząstka grawitacyjna C, która normalnie uderzyłaby w A, zostaje zablokowana przez B, jednak inna cząstka grawitacyjna D, która normalnie ominęłaby A, zostaje ku niemu odbita przez zderzenie z B, zastępując tym samym cząstkę C. Zatem, jeżeli zderzenia są w pełni sprężyste, odbite cząstki pomiędzy A i B skompensują efekt cienia. Aby otrzymać ujemną siłę wypadkową, należy założyć, że zderzenia nie są w pełni elastyczne, lub przynajmniej, że odbite cząstki są spowolnione. Skutkowałoby to wychodzącym od A strumieniem o zmniejszonym pędzie, oraz zmierzającym ku A strumieniem o normalnym pędzie, przez co powstawałaby siła skierowana ku środkowi A (P3). Przy takich założeniach, odbite cząstki nie kompensowałyby efektu cienia w przypadku dwóch ciał, ponieważ odbity strumień byłby słabszy niż nadbiegający.

Prawo odwrotności kwadratu

P4: Zależność odwrotności kwadratu

Ponieważ zakłada się, że część lub wszystkie cząstki grawitacyjne, skupiające się na obiekcie, są albo absorbowane, albo spowalniane przez obiekt, pociąga to za sobą konsekwencję, że intensywność strumienia, emanującego z kierunku masywnego obiektu, jest mniejsza, niż intensywność strumienia skupiającego się na obiekcie. Możemy wyobrazić sobie to niezrównoważenie przepływu - a tym samym siły wywieranej na dowolny obiekt w otoczeniu - rozłożone na sferycznej powierzchni, wyśrodkowanej na obiekcie (P4). Niezbalansowanie pędu przepływu przez całą sferę otaczającą obiekt jest niezależne od wielkości sfery, podczas gdy powierzchnia sfery rośnie proporcjonalnie do kwadratu promienia. Zatem niezbalansowanie pędu na jednostkę powierzchni maleje wraz z odwrotnością kwadratu odległości.

Źródła (drugorzędne)

• Aronson, S.. The gravitational theory of Georges-Louis Le Sage. „The Natural Philosopher”. 3, s. 51–74, 1964. 
• Bellone, E.. Classic and non-intentional consequences of some newtonian problems. „Mem. Società Astronomica Italiana”. 62 (3), s. 477–485, 1991. Bibcode: 1991MmSAI..62..477B. 
• Borzeszkowski, H.-H., Chrobok, T., Treder, H.-J.. Screening and absorption of gravitation in pre-relativistic and relativistic theories. „Proceedings of the 18th Course of the School on Cosmology and Gravitation”, s. 1–37, 2004. DOI: 10.1007/978-1-4020-2242-5_1. arXiv:gr-qc/0310081. Bibcode: 2004grco.book....1V. 
• Chabot, H.. Nombre et approximations dans la théorie de la gravitation de Lesage. „Actes des Journées de Peirescq "La pensée numérique", Sciences et Techniques en Perspective, 2ème série”. 8, s. 179–198, 2004. 
• Corry, L.. David Hilbert between Mechanical and Electromagnetic Reductionism. „Archive for History of Exact Sciences”. 53 (6), s. 489–527, 1999. DOI: 10.1007/s004070050005. 
• Drude, Paul. Ueber Fernewirkungen. „Annalen der Physik”. 298 (12), s. I–XLIX, 1897. DOI: 10.1002/andp.18972981220. Bibcode: 1897AnP...298D...1D. 
• Gravity in the century of light: sources, construction and reception of Le Sage's theory of gravitation, [w:] J.C.J.C. Evans J.C.J.C., Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation, Montreal: C. Roy Keys Inc., 2002, s. 9–40 .
• The search for gravitational absorption in the early 20th century. W: Martins, de Andrade, R.: The Expanding Worlds of General Relativity (Einstein Studies). T. 7. Boston: Birkhäuser, 1999, s. 3–44.
• Gravitational absorption according to the hypotheses of Le Sage and Majorana. W: Martins, de Andrade, R.: Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation. Montreal: C. Roy Keys Inc., 2002, s. 239–258.
• J. Playfair. Notice de la Vie et des Ecrits de George Louis Le Sage. „Edinburgh Review”, s. 137–153, 1807.  English summary of Prévost (1805).
• PierreP. Prévost PierreP., Notice de la Vie et des Ecrits de George Louis Le Sage, Geneva & Paris: J.J. Paschoud, 1805 .
• J. S. Rowlinson. Le Sage's Essai de Chymie Méchanique. „Notes Rec. R. Soc. London”. 57 (1), s. 35–45, 2003. DOI: 10.1098/rsnr.2003.0195. 
• Taylor, W. B.. Kinetic Theories of Gravitation. „Annual report of the Smithsonian institution”. 31, s. 205–282, 1876. 
• Wolf, R.. George-Louis Le Sage. „Biographien zur Kulturgeschichte der Schweiz”. 4, s. 173–192, 1862. Orell, Füssli & co.. 
• H.H. Zehe H.H., Die Gravitationstheorie des Nicolas Fatio de Duillier, Hildesheim: Gerstenberg, 1980, ISBN 3-8067-0862-2 .
• Zenneck, J.. Gravitation. „Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen”. 5 (1), s. 25–67, 1903. Leipzig. DOI: 10.1007/978-3-663-16016-8_2.