Teoria liczb
Zasugerowano, aby zintegrować ten artykuł z artykułem Arytmetyka teoretyczna (dyskusja).
|
Teoria liczb – dziedzina matematyki badająca własności niektórych typów liczb[a]. Początkowo analizowała tylko liczby naturalne i wymierne, później rozszerzając zakres o inne liczby rzeczywiste, zwłaszcza algebraiczne[1]. Przynajmniej częściowo jest zaliczana do matematyki dyskretnej[2].
Jest to jedna z najstarszych dziedzin matematyki obok geometrii; obie dyscypliny od starożytności nie przestają na siebie oddziaływać. Rozwój teorii liczb miał też wpływ na inne gałęzie matematyki jak algebra[1] – w tym ogólna algebra przemienna – oraz geometria algebraiczna, analiza zespolona i probabilistyka[3]. Kierunek zastosowań jest też odwrotny: teoria liczb sama skorzystała z osiągnięć algebry, geometrii algebraicznej i probabilistyki[1]. Niektóre z wykorzystywanych metod są zaawansowane jak np. algebra homologiczna[1] i abstrakcyjna analiza harmoniczna[3]. Teoria liczb obfituje w problemy otwarte postawione elementarnie – tj. zrozumiałe dla laików, nawet dla dzieci – ale czekające na rozwiązanie wyjątkowo długo, czasem stulecia. Niektóre z pytań zadanych w XVIII wieku – jak hipoteza Goldbacha i hipoteza prostopadłościanu idealnego – do dzisiaj pozostają bez odpowiedzi. Teorią liczb zajmowali się matematycy zaliczani do najwybitniejszych w historii jak Leonhard Euler, Carl Friedrich Gauss i Bernhard Riemann; wkład w tę dziedzinę nagradzano też najwyższymi zaszczytami w matematyce jak Medal Fieldsa, Nagroda Abela czy Medal Copleya przyznawany także innym naukowcom. Istnieją również nagrody poświęcone tej konkretnej dziedzinie – odpowiednie kategorie Nagrody Cole’a i Nagrody Fermata. Teorię liczb nazywano „królową matematyki”[3][4].
W II połowie XX wieku znaleziono zastosowania tej dyscypliny w kryptologii i fizyce matematycznej, zwłaszcza kwantowej teorii pola, teorii strun oraz teorii kwantowego chaosu[5]. Powstało całe czasopismo naukowe poświęcone związkom teorii liczb z fizyką[6]. Ta dziedzina matematyki wywarła też pewien wpływ na popkulturę; amatorskie badania wielkiego twierdzenia Fermata są motywem powieści młodzieżowej Szatan z siódmej klasy Kornela Makuszyńskiego (1937).
Podział teorii liczb
Główne działy teorii liczb to[7]:
- elementarna teoria liczb,
- algebraiczna teoria liczb,
- analityczna teoria liczb,
- multiplikatywna teoria liczb,
- addytywna teoria liczb,
- geometryczna teoria liczb,
- probabilistyczna teoria liczb,
- kombinatoryczna teoria liczb.
Elementarna teoria liczb jest jej najstarszym działem; nie stosuje się w niej metod teorii funkcji analitycznych. Do najważniejszych osiągnięć elementarnej teorii liczb należą dowody Erdősa i Selberga twierdzenia o dystrybucji liczb pierwszych (ich dowody były niezależne, ale oba oparte na lemacie Selberga). Teoria liczb zajmuje się również rozwiązywaniem równań w dziedzinie liczb naturalnych, całkowitych, wymiernych, algebraicznych (całkowitych i wymiernych) oraz (od niedawna) liczb p-adycznych.
Do analitycznej teorii liczb zalicza się:
- teorię liczb pierwszych – część multiplikatywnej teorii liczb;
- twierdzenia jak to Lagrange’a: każda liczba naturalna jest sumą czterech kwadratów liczb całkowitych; wynik ten należy do addytywnej teorii liczb, ale także do teorii elementarnej;
- teorię liczb niewymiernych, mającą zastosowania w teorii równań diofantycznych, które z kolei są częścią algebraicznej teorii liczb.
Historia
Starożytność i średniowiecze
Początki teorii liczb sięgają starożytności; przykładowo starożytni mieszkańcy Mezopotamii oraz Egiptu mogli rozważać problem trójek pitagorejskich. Największe postępy w tej dziedzinie zrobiła jednak kultura starogrecka. Odnotowano serię postępów na przestrzeni niecałego tysiąclecia, od okresu klasycznego do czasów cesarskiego panowania rzymskiego:
- Pitagorejczycy opisali:
- liczby niewymierne na przykładzie pierwiastka kwadratowego z dwójki;
- liczby zaprzyjaźnione;
- o niewymierności pierwiastków z liczb naturalnych pisał też potem Teodor z Cyreny;
- Euklides z Aleksandrii w dziele Elementy wyłożył:
- algorytm Euklidesa znajdowania największego wspólnego dzielnika,
- dowód, że istnieje nieskończenie wiele liczb pierwszych[1];
- zasadnicze twierdzenie arytmetyki oparte o lemat Euklidesa;
- sposób znajdowania niektórych liczb doskonałych;
- Eratostenesowi przypisuje się metodę znajdowania liczb pierwszych: sito Eratostenesa;
- Diofantos został upamiętniony nazwą równań diofantycznych[1].
Teorią liczb mógł się zajmować także Archimedes, ale raczej marginesowo; nowe odkrycia historyczne mogą ten pogląd zmienić.
Równolegle rozwijano matematykę w Indiach, w sposób komplementarny do tego greckiego i znaczący dla teorii liczb. Systemy pozycyjne uprościły wiele obliczeń i pozwoliły na sformułowanie cech podzielności liczb całkowitych. Matematycy chińscy rozważali za to układy kongruencji, na temat których udowodnili chińskie twierdzenie o resztach. Uczeni arabscy mieli w tę dziedzinę ograniczony wkład – w matematyce skupili się na trygonometrii i algebrze[8], choć ta druga dziedzina później wpłynęła na rozwój teorii liczb.
W XIII-wiecznych Włoszech kupiec Leonardo Fibonacci podał jedną z metod generowania trójek pitagorejskich, a oprócz tego opisał ciąg Fibonacciego, również istotny z punktu widzenia teorii liczb. Problem nieskończoności liczb pierwszych w tym ciągu w lutym 2022 pozostaje otwarty.
XVII wiek

XVII wiek to umowny początek nowożytnej teorii liczb i jej statusu samodzielnej nauki[8]. Rozwijał ją wtedy Pierre de Fermat i miał w tej dziedzinie co najmniej pięć znaczących osiągnięć:
- małe twierdzenie Fermata[1], na którym opiera się m.in. test pierwszości Fermata;
- hipoteza zwana Wielkim Twierdzeniem Fermata, udowodniona potem w XX wieku[1];
- badania liczb Fermata; wysunął hipotezę, że wszystkie z nich są liczbami pierwszymi. Leonhard Euler obalił ją kontrprzykładem, a do tej pory (luty 2022) nie znaleziono żadnego dalszego przykładu liczby pierwszej Fermata. Jest to sugestia, że prawdziwe może być twierdzenie przeciwne – brak liczb pierwszych Fermata dalszych niż te, które sam znalazł;
- twierdzenie Fermata o sumie dwóch kwadratów;
- algorytm Fermata faktoryzacji liczb całkowitych.
W tym samym stuleciu:
- Marin Mersenne badał pewien ciąg liczbowy, nazwany potem liczbami Mersenne’a. Znalazł w nim nowe liczby pierwsze; w dalszych stuleciach znajdowano w nim jeszcze więcej takich liczb, co prowadzi do pytania, czy jest ich nieskończenie wiele. Znaleziono też związek liczb pierwszych Mersenne’a z rozważanymi od starożytności liczbami doskonałymi[9];
- John Pell rozważał także pewne kwadratowe równanie diofantyczne nazwane potem od jego nazwiska (równanie Pella). Zrobił to jako pierwszy w Europie, choć już tysiąclecie wcześniej badali je matematycy indyjscy.
XVII wiek to także narodziny nowych dziedzin matematyki, które okazały się istotne dla teorii liczb:
- geometria analityczna dała nową, graficzną perspektywę na pewne fakty i problemy. Przykładowo rozwiązania równań diofantycznych to punkty kratowe odpowiednich krzywych itp. figur w kartezjańskim układzie współrzędnych; trójki pitagorejskie odpowiadają punktom kratowym okręgów o całkowitym promieniu. Geometria analityczna jest też korzeniem geometrii algebraicznej, blisko związanej z teorią liczb;
- analiza poszerzyła zakres badań arytmetyki i jej metody. Wprowadzona tam podstawa logarytmu naturalnego (e) stała się przedmiotem dociekań, a nowe tożsamości związane z liczbą pi (π) pozwoliły potem udowodnić jej niewymierność. Związki teorii liczb z analizą zacieśniły się później w XIX wieku;
- probabilistyka dostarczyła teorii liczb nowych metod[1], m.in. algorytmów.
XVIII wiek
W XVIII wieku Leonhard Euler – jak wspomniano wyżej – obalił hipotezę Fermata o liczbach nazwanych jego nazwiskiem[9]. Oprócz tego Euler:
- uogólnił małe twierdzenie Fermata na inne dzielniki (moduły), niekoniecznie pierwsze;
- podał rekordowo dużą liczbę pierwszą;
- w 1744 udowodnił, że suma odwrotności liczb pierwszych jest nieskończona (jest to szereg rozbieżny)[10]; rozszerzył tym znany wcześniej fakt o nieskończoności liczb pierwszych;
- wykazał, że każda parzysta liczba doskonała ma związek z liczbami pierwszymi Mersenne’a[9];
- udowodnił, że podstawa logarytmu naturalnego (e) jest niewymierna. Był to pierwszy dowód niewymierności od czasów starożytnych;
- wprowadził stałą nazywaną od jego nazwiska, co zrobił potem niezależnie Lorenzo Mascheroni. Wymierność stałej γ była potem długo badana przez matematyków, a w lutym 2022 roku pozostaje to problem otwarty;
- wysunął pewną hipotezę o sumach potęg, jednak obalono ją w XX wieku metodami komputerowymi.
Postępy poczynili też inni matematycy:
- W 1719 roku Paul Halcke podał pierwszy przykład cegiełki Eulera, tj. prostopadłościanu o całkowitych krawędziach i przekątnych ścian. Jego rozwiązanie odpowiedniego układu równań diofantycznych to (44,117,240). Doprowadziło to do pytania o prostopadłościan idealny, mający dodatkowo całkowitą przekątną (główną); w lutym 2022 problem pozostaje otwarty.
- Johann Heinrich Lambert udowodnił niewymierność liczby pi (π).
- Christian Goldbach wysunął pewną hipotezę o liczbach pierwszych, nazwaną potem hipotezą Goldbacha. W XXI wieku ogłoszono dowód jej słabszej wersji, w lutym 2022 czekający na pełną weryfikację.
- Joseph Louis Lagrange udowodnił twierdzenie nazwane jego nazwiskiem. Mówi ono, że każda liczba naturalna jest sumą czterech kwadratów naturalnych;
- Edward Waring rozwinął też badania problemu Waringa. Jego uczeń wysunął hipotezę nazywaną twierdzeniem Wilsona; zostało udowodnione jeszcze w tamtym stuleciu przez Lagrange’a i jest warunkiem równoważnym pierwszości liczby naturalnej.
XIX wiek

XIX wiek to narodziny nowych gałęzi w teorii liczb:
- Carl Friedrich Gauss otworzył algebraiczną teorię liczb, wprowadzając kongruencje, dowodząc lematu Gaussa i prawa wzajemności reszt kwadratowych[1];
- Bernhard Riemann i August Ferdinand Möbius to pionierzy analitycznej teorii liczb, w której wysunięto m.in. hipotezę Riemanna;
- Joseph Liouville udowodnił istnienie liczb przestępnych. Charles Hermite udowodnił, że należy do nich e (stała Eulera), a Ferdinand Lindemann wykazał przestępność pi (π). Pokrewnym tematem jest aproksymacja diofantyczna liczb niewymiernych, o której Peter Gustav Lejeune Dirichlet udowodnił znaczące twierdzenie;
- Hermann Minkowski zapoczątkował geometrię arytmetyczną[1].
Rozwinięto też „klasyczne” badania liczb naturalnych:
- w 1850 Pafnutij Czebyszow udowodnił postulat Bertranda o rozmieszczeniu liczb pierwszych[11], przez co wynik ten nazwano również twierdzeniem Czebyszowa.
- Eugène Charles Catalan wysunął też hipotezę o nierozwiązywalności pewnego równana diofantycznego. Na rozstrzygnięcie czekała do XXI wieku.
- Twierdzenie Gaussa-Wantzela pokazało związek teorii liczb z geometrią płaską (planimetrią), a konkretniej teorią konstrukcji klasycznych. Problem liczb pierwszych Fermata okazał się istotny dla konstruowalności wielokątów foremnych.
Ogłoszone na koniec stulecia 23 problemy Hilberta zawierały kilka pytań z teorii liczb jak hipotezy Riemanna i Golbacha.
XX wiek
Postęp w teorii liczb naturalnych był wieloraki – rozwiązano niektóre stare problemy oraz postawiono nowe:
- Najpóźniej wtedy sformułowano hipotezę o nieskończoności bliźniaczych liczb pierwszych. Viggo Brun zredukował ten problem do badania wymierności stałej nazwanej od jego nazwiska (B2).
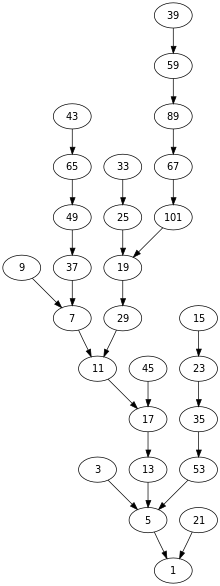
- Pojawił się też problem Collatza o zachowaniu pewnej funkcji lub równoważnie – rodziny ciągów liczb naturalnych.
- Srinivasa Ramanujan zainspirował badania liczb taksówkowych – pewnego rodzaju sum dwóch sześcianów naturalnych;
- Hillel Furstenberg zastosował w teorii liczb topologię, podając nowy dowód twierdzenia Euklidesa o nieskończoności liczb pierwszych.
- Znaczące osiągnięcia przyniosły też obliczenia komputerowe – m.in.:
- obaliły hipotezę Pólyi o własnościach czynników pierwszych (1958);
- obaliły hipotezę Eulera uogólniającą wielkie twierdzenie Fermata (1966);
- rozwiązały jedno z sześciennych równań diofantycznych: x3+y3+z3 = 30 (1999)[12].
- W latach 90. Andrew Wiles udowodnił wielkie twierdzenie Fermata po przeszło 300 latach zmagań matematyków z tym problemem.
- Również w tamtej dekadzie Peter Shor opublikował nowy algorytm faktoryzacji, aktywnie badany przez informatykę kwantową.
- W XX wieku rozwinięto też sprawdzanie pierwszości, opracowując algorytmy o coraz lepszej złożoności obliczeniowej.
Naświetlono również same fundamenty arytmetyki liczb naturalnych. Kurt Gödel w swoim pierwszym twierdzeniu o niezupełności wykazał, że nie może ona być jednocześnie zupełna i niesprzeczna. Wśród nowo poznanych liczb pierwszych znalazły się osobliwości jak liczba Belfegora. Nie dość, że w zapisie dziesiętnym jest palindromem, to jeszcze zawiera w nim liczbę bestii (666), a liczba zer po obu stronach tego symbolu wynosi 13 – także oznakę nieszczęść.
Posunięto też badania nad niewymiernością i przestępnością:
- w 1934 udowodniono twierdzenie Gelfonda-Schneidera, rozwiązujące jeden z problemów Hilberta[13];
- w latach 70. Mitchell Jay Feigenbaum w swoich pracach nad teorią chaosu wprowadził dwie nowe stałe liczbowe, nazwane jego nazwiskiem (α i δ). Ich wymierność stała się przedmiotem analiz;
- w 1979 roku Roger Apéry udowodnił, że suma ζ(3), nazwana potem stałą Apéry’ego, jest niewymierna.
Wiek XX przyniósł też zastosowania dla teorii liczb – w latach 70. rozbudowano kryptografię klucza publicznego, w tym szyfr RSA; opisano także pierwsze związki teorii liczb z fizyką.
Stulecie zwieńczono ogłoszeniem listy siedmiu problemów millenijnych. Co najmniej dwa z nich mają bezpośredni związek z teorią liczb – jak hipoteza Riemanna.
XXI wiek

Nowe tysiąclecie przyniosło między innymi:
- dowód hipotezy Catalana; zrobił to Preda Mihăilescu w 2002 roku;
- twierdzenie Greena-Tao o ciągach arytmetycznych wśród liczb pierwszych.
Ogłoszono też pewne sukcesy, które w lutym 2022 dalej czekają na pełną weryfikację, choć są aktywnie badane przez społeczność akademicką:
- Shinichi Mochizuki w 2012 roku przedstawił pracę, która jego zdaniem dowodzi hipotezy abc;
- Harald Helfgott w 2013 roku zaproponował dowód słabej hipotezy Goldbacha.
W 2018 roku Michael Atiyah ogłosił, że udało mu się udowodnić hipotezę Riemanna i zaprezentował swoją próbę dowodu. Została ona odrzucona przez matematyków jako błędna. Wiele innych problemów teorii liczb – także postawionych elementarnie – w lutym 2022 pozostaje nierozwiązanych. Niektóre z nich to:
- kwestia liczb pierwszych niektórych typów. Nie wiadomo, czy istnieje nieskończenie wiele liczb pierwszych Fibonacciego, Mersenne’a, Germain, bliźniacznych, czworaczych ani czy istnieją jakiekolwiek liczby pierwsze w ciągu Fermata poza pięcioma początkowymi wyrazami. Problem liczb pierwszych Mersenne’a ma konsekwencje dla teorii parzystych liczb doskonałych – nie wiadomo, czy jest ich nieskończenie wiele;
- hipoteza Goldbacha;
- pytania dotyczące liczb całkowitych, ale nie wprost liczb pierwszych, np. prostopadłościan idealny i problem Collatza. Nie wiadomo też, czy istnieje jakakolwiek nieparzysta liczba doskonała ani czy ciąg liczb zaprzyjaźnionych jest skończony;
- wymierność niektórych stałych jak Eulera-Mascheroniego (γ), stałe Feigenbauma (α i δ) czy wartości funkcji dzeta Riemanna dla liczb nieparzystych większych od trzech: ζ(2n+1), n>1. Niektóre problemy dotyczące liczb pierwszych sprowadzono do pytania o wymierność stałych Bruna jak B2 i B4;
- przestępność niektórych liczb niewymiernych jak stała Apéry’ego ζ(3);
- zagadnienia obliczeniowe, np. czy faktoryzacja liczb całkowitych należy do problemów klasy P – tj. czy jej złożoność może być wielomianowa.
Teoria liczb w Polsce

Wśród matematyków polskich znaczące wyniki w teorii liczb uzyskali między innymi:
- Wacław Sierpiński[1] – zob. liczby Sierpińskiego, stała Sierpińskiego;
- Stanisław Ulam – por. spirala Ulama;
- Andrzej Schinzel;
- Henryk Iwaniec – za swoje badania został nagrodzony m.in. Nagrodą Shawa w dziedzinie matematyki (2015);
- Stanisław Knapowski.
Posiadaczem szeregu wyliczeniowych rekordów światowych jest Jarosław Wróblewski. Teorii liczb jest poświęcone polskie czasopismo „Acta Arithmetica”, założone w latach 30. XX w., później wydawane przez Instytut Matematyczny Polskiej Akademii Nauk (IM PAN).
Z polską narodowością i nauką polską bywa też wiązany Franz Mertens – pracownik m.in. Uniwersytetu Jagiellońskiego, zajmujący się analityczną teorią liczb. Jego hipoteza Mertensa, implikująca hipotezę Riemanna, okazała się jednak fałszywa – obalono ją w latach 80. XX w..
Ludzie
Euklides z Aleksandrii (IV w. p.n.e.),
Pierre de Fermat (XVII w.),
Bernhard Riemann (XIX w.),
Do znaczących naukowców w tej dziedzinie należą[1]:
- Euklides z Aleksandrii (IV–III w. p.n.e.),
- Diofantos (III w. n.e.),
- Leonardo Pisano vel Fibonacci (1175–1250),
- Marin Mersenne (1588–1648),
- Pierre de Fermat (1601–1665),
- John Pell (1611–1685),
- Christian Goldbach (1690–1764),
- Leonhard Euler (1707–1783),
- Johann Heinrich Lambert (1728–1777),
- Adrien-Marie Legendre (1752–1833),
- Sophie Germain (1776–1831),
- Carl Friedrich Gauss (1777–1855),
- August Ferdinand Möbius (1790–1868),
- Carl Gustav Jakob Jacobi (1804–1851),
- Peter Gustav Lejeune Dirichlet (1805–1859),
- Gotthold Eisenstein[1],
- Joseph Liouville (1809–1882),
- Ernst Eduard Kummer (1810–1893),
- Eugène Charles Catalan (1814–1894),
- Pafnutij Czebyszow (1821–1894),
- Joseph Louis François Bertrand (1822–1900),
- Leopold Kronecker (1823–1891),
- Bernhard Riemann (1826–1866),
- Richard Dedekind (1831–1916),
- Ferdinand Lindemann (1852–1939),
- David Hilbert (1862–1943),
- Hermann Minkowski (1864–1909),
- Viggo Brun (1882–1978),
- Wacław Sierpiński (1882–1969),
- George Pólya (1887–1985),
- Srinivasa Ramanujan (1887–1920),
- André Weil (1906–1998),
- Hillel Furstenberg (1935–),
- Andrew Wiles (1953–),
- Preda Mihăilescu (1955–),
- Terence Tao (1975–).
Uwagi
- ↑ liczby kardynalne i porządkowe są badane przez teorię mnogości.
Przypisy
- ↑ a b c d e f g h i j k l m n Liczb teoria, [w:] Encyklopedia PWN [online] [dostęp 2022-02-15].
- ↑ Eric W. Weisstein, Discrete Mathematics, [w:] MathWorld [online], Wolfram Research (ang.). [dostęp 2022-02-15].
- ↑ a b c Iwaniec 1993 ↓, s. 698.
- ↑ 22·5·7 urodziny, [w:] pismo „Delta” [online], deltami.edu.pl, marzec 2022, ISSN 0137-3005 [dostęp 2022-03-15] (pol.).
- ↑
 Piotr Sułkowski, Fizyka i teoria liczb, 3 września 2016 [dostęp 2022-02-15].
Piotr Sułkowski, Fizyka i teoria liczb, 3 września 2016 [dostęp 2022-02-15]. - ↑
 Communications in Number Theory and Physics (ang.), intlpress.com [dostęp 2022-02-15].
Communications in Number Theory and Physics (ang.), intlpress.com [dostęp 2022-02-15]. - ↑ Iwaniec 1993 ↓, s. 698–726.
- ↑ a b Iwaniec 1993 ↓, s. 693.
- ↑ a b c Iwaniec 1993 ↓, s. 694.
- ↑ Iwaniec 1993 ↓, s. 720.
- ↑ Iwaniec 1993 ↓, s. 721.
- ↑ Mariusz Skałba, Popularne książki Sierpińskiego, [w:] pismo „Delta” [online], deltami.edu.pl, marzec 2022, ISSN 0137-3005 [dostęp 2022-03-15] (pol.).
- ↑ Iwaniec 1993 ↓, s. 713.
Bibliografia
- Henryk Iwaniec: Teoria liczb [w:] Leksykon matematyczny. Warszawa: Wydawnictwo „Wiedza Powszechna”, 1993. ISBN 83-214-0783-8.
Linki zewnętrzne
 Wacław Sierpiński, Teoria liczb, pldml.icm.edu.pl [dostęp 2022-02-16] – monografia z 1950 roku.
Wacław Sierpiński, Teoria liczb, pldml.icm.edu.pl [dostęp 2022-02-16] – monografia z 1950 roku.
Media użyte na tej stronie
Autor: David Eppstein, Licencja: CC0
Pell's equation x2 − 2y2 = 1 and its solutions, the integer points on the hyperbola defined by the equation. The of x-coordinates of the solutions, 1, 3, 17, ..., are given by every other term in the sequence of Pell numbers.
Autor:
Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).
[1], Licencja: CC BY-SA 4.0Statue in honor of Euclid in the Oxford University Museum of Natural History
Sir Andrew Wiles at 61st Birthday conference for P. Deligne, held at the Institute for Advanced Study, Princeton, October 2005.
Plimpton 322, Babylonian tablet listing pythagorean triples
Autor: William Demchick (Kiwi128), Licencja: CC BY 3.0
A graphic that describes Euler's constant visually. The area that is blue is equal to Euler's constant if the process is continued; more concretely, this is taking the limit as x -> ∞.
Regular heptagon
Directed graph showing the orbits of the odd numbers less than 50 (with the exceptions of 27, 31, 41, and 47, because they would make it too tall) under the Collatz map.
For a larger graph, see :Image:Collatz-graph-300.svg.
Created with Graphviz, with the help of this Python program:
dotfile = file('collatz-graph.dot', 'w')
limit = 50
def f(n):
while n % 2 == 0: # divide by 2 until it's odd
n /= 2
n = 3*n + 1
while n % 2 == 0:
n /= 2
return n
explored = set([1,27,31,41,47])
dotfile.write('digraph {\n')
for n in range(3, limit, 2): # odd numbers
while n not in explored:
dotfile.write(str(n) + ' -> ')
explored.add(n)
n = f(n)
dotfile.write(str(n) + ';\n')
dotfile.write('}\n') Autor: Cmglee, Licencja: CC BY-SA 4.0
Isometric projections to scale of all five primitive Euler bricks with dimensions under 1000 by CMG Lee.
Почтовая марка Чехии 2000 года к Всемирному году математики.
This is an Ulam spiral of 150 x 150 dots, with differing widths. It's a copy of File:Spirale_Ulam_150.jpg only in SVG format.
Tête de Pierre de Fermat


















