Teoria węzłów
Teoria węzłów – dział topologii zajmujący się badaniem związanym z zagadnieniami i własnościami węzłów i splotów, a także supłów zaproponowanych przez Johna H. Conwaya[1].
Węzły to zamknięte pętle umieszczone w przestrzeni trójwymiarowej, czyli zaplątane krzywe z połączonymi końcami. Mówiąc inaczej węzeł to homeomorficzny obraz okręgu zanurzonego w przestrzeni 3-wymiarowej R3.
Splot to suma skończonej ilości węzłów wzajemnie rozłącznych, zwanych składowymi splotu, które mogą być zasupłane i splecione ze sobą. Węzeł jest splotem o jednej składowej, a splot jest sumą okręgów parami rozłącznych. Kilka węzłów tworzy splot, a poszczególne węzły nazywane są jego ogniwami. Sam węzeł zatem jest szczególnym przypadkiem splotu.
Podstawowym problemem teorii węzłów jest klasyfikacja węzłów i ich rozróżnianie.
Najprostszym węzłem jest tzw. węzeł trywialny czyli okrąg (inaczej pętla trywialna, zwany też niewęzłem i oznaczony przez 01). Pełną klasyfikację węzłów do 9. rzędu opracował w końcu lat 20. XX wieku Kurt Reidemeister[2][3].
W 1928 roku James W. Alexander przyporządkował węzłom pewne wielomiany[4].
W 1984 roku nowozelandzki matematyk Vaughan F. R. Jones odkrył niezmiennik i oznaczył V, a obecnie znany jest jako wielomian Jonesa. Jones przypisał każdemu splotowi zorientowanemu wielomian Laurenta, przez co odkrył zaskakujące związki między algebrą operatorów i teorią węzłów i podał proste niezmienniki charakteryzujące węzły. Za prace nad teorią węzłów otrzymał w 1990 roku Medal Fieldsa.
W 1985 roku grupa matematyków w składzie: J. Hoste, A. Ocneanu, K. Millett, P. J. Freyd, W. B. R. Lickorish, D. N. Yetter[5] oraz w 1987 roku Józef Przytycki, Paweł Traczyk[6], odkryła inny niezmiennnik zwany wielomianem HOMFLY-PT (nazwa od inicjałów autorów).
Zastosowania
Teoria węzłów odgrywa istotną rolę przy badaniu rozmaitości trójwymiarowych.
Teoria węzłów znalazła zastosowanie w rozmaitych dziedzinach życia takich jak analiza obwodów elektrycznych, kryptografia czy mechanika statystyczna. W biologii molekularnej i chemii supramolekularnej węzłów używa się też do opisu struktur DNA i białek.
Zobacz też
Przypisy
- ↑ Conway J.: An enumeration of knots and links and some of their related properties. Computational Problems in Abstract Algebra, Proc. Conf. Oxford 1967 (Ed. J. Leech), 329-358. New York: Pergamon Press, 1970
- ↑ Reidemeister K.: Knotentheorie. Berlin: Springer Verlag, 1932
- ↑ Węzłów teoria, [w:] Encyklopedia PWN [online] [dostęp 2021-07-23].
- ↑ Alexander, J. W. (1928). "Topological invariants of knots and links". Trans. Amer. Math. Soc. 30 (2): 275–306. doi:10.2307/1989123.
- ↑ J. Hoste, A. Ocneanu, K. Millett, P. Freyd, W. B. R. Lickorish and D. Yetter, A new polynomial invariant of knots and links, Bull. Amer. Math. Soc. 12 (1985) 239-246.
- ↑ J. Przytycki and P. Traczyk, Conway Algebras and Skein Equivalence of Links, Proc. Amer. Math. Soc. 100 (1987) 744-748.
Bibliografia
Książki
- Roman Duda, Wprowadzenie do topologii, Warszawa: Państwowe Wydawnictwo Naukowe, 1986, ISBN 83-01-05714-9, OCLC 835906814.
- Louis H. Kauffman, Knots and Physics, wyd. 2nd ed, Singapore: World Scientific Publishing Co Ltd, 1993, ISBN 981-02-1656-4, OCLC 30675365.
- Charles Livingston, Knot Theory, Washington, DC: The Mathematical Association of America, 1993, ISBN 0-88385-027-3.
- Józef H. Przytycki, Węzły: Podejście kombinatoryczne do teorii węzłów, Warszawa: „Script”, 1995, ISBN 83-904564-0-0, OCLC 835322498.
- Hugo Steinhaus, Kalejdoskop matematyczny, Józef Łukaszewicz (oprac.), Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1989, ISBN 83-02-02326-4, OCLC 749380384.
Czasopisma
- Lee Neuwirth, The Theory of Knots, Scientific American, No. 6, 1979, s. 84-96.
- F. Y. Wu, Knot theory and statistical mechanics, Reviews of Modern Physics, Vol. 64, No. 4, October 1992.
Linki zewnętrzne
- Eric W. Weisstein, Knot Theory, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12] (ang.).
Media użyte na tej stronie
Autor: YAMASHITA Makoto I mainly contribute math graphics. My home wiki is Japanese Wikipedia (my user page there), but I occasionally contribute to English Wikipedia as en:User:Makotoy and other WikiMedia projects., Licencja: CC-BY-SA-3.0
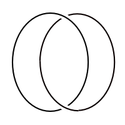
This picture shows the regular presentation of Hopf link. The link is a basic example of nontrivial link with more than one component in knot theory (mathematics). The regular representation, commonly used in the theory to indicate knots and links, represents projection onto 2-dimensional plane of the link. At each intersection, the below string is split a bit to indicate how the strings are arranged at that point.
Autor: Ɯ, Licencja: CC BY-SA 3.0
Partial Knot Diagram for Skein Relation: Horizontal. No orientation indicated.
Autor: Thomas Steiner, Licencja: CC-BY-SA-3.0
Projektion des Kleeblattknotens (halber Schlag)