Trójkąt
 | |
| Liczba boków | 3 |
|---|---|
| Liczba przekątnych | 0 |
| Symbol Schläfliego | {3} (trójkąt równoboczny) |
| Kąt wewnętrzny | 60° (trójkąt równoboczny) |
Trójkąt – wielokąt o trzech bokach[1]. Trójkąt to najmniejsza (w sensie inkluzji) figura wypukła i domknięta, zawierająca pewne trzy ustalone i niewspółliniowe punkty płaszczyzny (otoczka wypukła wspomnianych trzech punktów).
Odcinki tworzące łamaną nazywamy bokami, punkty wspólne sąsiednich boków nazywamy wierzchołkami trójkąta[1][2]. Każdy trójkąt jest jednoznacznie wyznaczony przez swoje wierzchołki.
Często dla wygody jeden z boków trójkąta nazywa się podstawą, a pozostałe – ramionami[1].
W każdym trójkącie suma miar kątów wewnętrznych między bokami wynosi 180°[1], zaś długości boków muszą spełniać pewne zależności (patrz dalej).
Rodzaje
Trójkąty można dzielić ze względu na długości ich boków oraz ze względu na miary ich kątów.
Przy podziale ze względu na boki wyróżnia się:
- trójkąt różnoboczny ma każdy bok innej długości;
- trójkąt równoramienny ma dwa boki tej samej długości[1];
- trójkąt równoboczny ma wszystkie trzy boki tej samej długości[1]; wszystkie jego kąty są tej samej miary.
 | 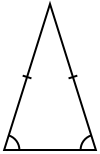 |  |
| równoboczny | równoramienny | różnoboczny |
Przy podziale ze względu na kąty wyróżnia się:
- trójkąt ostrokątny, którego wszystkie kąty wewnętrzne są ostre[1];
- trójkąt prostokątny to taki, w którym jeden z kątów wewnętrznych jest prosty[1] (a więc pozostałe sumują się do kąta prostego); boki tworzące kąt prosty nazywa się przyprostokątnymi, pozostały bok nosi nazwę przeciwprostokątnej[3]; przeciwprostokątna zawsze jest dłuższa od każdej przyprostokątnej;
- trójkąt rozwartokątny, którego jeden kąt wewnętrzny jest rozwarty[1].
 | 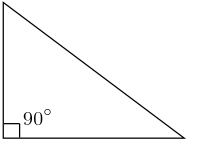 | 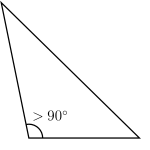 |
| ostrokątny | prostokątny | rozwartokątny |
Trójkąty można dzielić również ze względu na inne relacje równoważności, np. podobieństwo, przystawanie.
Ważne elementy
Wysokość trójkąta to prosta zawierająca jego wierzchołek i prostopadła do prostej zawierającej przeciwległy bok[3]. Słowem „wysokość” często też nazywany jest odcinek wysokości, łączący wierzchołek z punktem na prostej zawierającej przeciwległy bok; długość tego odcinka też nazywa się wysokością. Każdy trójkąt ma trzy wysokości, które przecinają się w punkcie zwanym ortocentrum tego trójkąta.
Środkowa trójkąta to prosta zawierająca wierzchołek trójkąta i środek przeciwległego boku[1]. Każdy trójkąt ma trzy środkowe, które przecinają się w jednym punkcie[1], będącym środkiem geometrycznym (barycentrum, lub błędnie środkiem masy lub środkiem ciężkości) trójkąta. Punkt ten dzieli każdą ze środkowych na dwie części, przy czym odcinek łączący barycentrum z wierzchołkiem jest dwa razy dłuższy od odcinka łączącego barycentrum ze środkiem boku.
Symetralna boku trójkąta to prosta prostopadła do tego boku i przechodząca przez jego środek[1]. Każdy trójkąt ma trzy symetralne boków, przecinające się w punkcie będącym środkiem okręgu opisanego na tym trójkącie[1].
Dwusieczne kątów wewnętrznych trójkąta przecinają się w punkcie, który jest środkiem okręgu wpisanego w ten trójkąt[1].
Symediana jest odbiciem środkowej w dwusiecznej wychodzącej z tego samego wierzchołka trójkąta.
Punkt Nagela – punkt, w którym przecinają się proste łączące wierzchołki z punktami styczności przeciwległych boków z odpowiednimi okręgami dopisanymi.
Punkt Gergonne'a – punkt przecięcia prostych łączących wierzchołki z punktami styczności przeciwległych boków do okręgu wpisanego w trójkąt.
Punkty Brocarda – w trójkącie ABC o bokach a, b, c znajduje się dokładnie jeden taki punkt P, że proste AP, BP, CP z bokami odpowiednio c, a, b tworzą równe kąty.
Punkt Fermata – punkt, którego suma odległości od wierzchołków trójkąta jest najmniejsza z możliwych.
 |  |  |  |
| wysokości i ortocentrum | środkowe i barycentrum | symetralne i okrąg opisany | dwusieczne i okrąg wpisany |
W każdym trójkącie punkty przecięcia: środkowych boków symetralnych boków wysokości (odpowiednio: barycentrum, środek okręgu opisanego, ortocentrum) leżą na jednej prostej, zwanej prostą Eulera. Ponadto
Pole powierzchni
Przyjmując dla trójkąta następujące oznaczenia:
- – długości boków;
- – wysokości opuszczone na boki odpowiednio
- – kąty leżące naprzeciw boków odpowiednio
- – pole powierzchni;
- – promień okręgu opisanego;
- – promień okręgu wpisanego;
- – połowa obwodu;
- – wysokości opuszczone na boki odpowiednio
dostaniemy następujące wzory na pole powierzchni[3]:
- (wzór Herona);
- (postać wyznacznikowa).
Z powyższych wzorów można wyprowadzić również następujące:
W geometrii analitycznej przyjmując dla wierzchołków trójkąta[3]
dostaniemy także następujące wzory:
- czyli
Środek geometryczny
Trójkąt, którego wierzchołki mają współrzędne kartezjańskie:
ma środek geometryczny (barycentrum) w punkcie:
Nierówność trójkąta
W każdym trójkącie o bokach, których długości wynoszą i zachodzi następująca nierówność, zwana nierównością trójkąta:
i analogicznie
Trójkąt o bokach, których długości wynoszą i istnieje wtedy i tylko wtedy, gdy spełnione są te trzy nierówności. Można je zapisać w równoważnej postaci:
Geometrie nieeuklidesowe
Na płaszczyźnie euklidesowej suma miar kątów wewnętrznych trójkąta jest równa kątowi półpełnemu, czyli
W geometriach innych niż euklidesowa suma kątów wewnętrznych nie musi wynosić 180°. Na przykład osoba, która pójdzie z bieguna północnego 10 tys. km na południe, 10 tys. km na zachód, a potem 10 tys. km na północ znajdzie się z powrotem na biegunie, choć dwukrotnie skręciła o 90°, więc trójkąt przez nią zakreślony ma sumę kątów większą niż 180°, a dokładnie 270°. Dzieje się tak, gdyż na sferze (dobre przybliżenie powierzchni geoidy) obowiązuje geometria eliptyczna, a nie euklidesowa. Dowód własności, że w przestrzeni euklidesowej suma kątów w trójkącie wynosi 180°, opiera się na piątym aksjomacie Euklidesa, który wyróżnia geometrię euklidesową spośród innych geometrii.
Zobacz też
- okrąg dziewięciu punktów
- sympleks
- trójkąt Penrose’a
- trójkąt sferyczny
- trójkąt wymierny
- twierdzenia: sinusów, cosinusów, tangensów
- twierdzenie Cevy, trygonometryczne
- twierdzenie Menelaosa
- twierdzenie Pitagorasa
- wzór Herona
Przypisy
Bibliografia
- Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), ISBN 83-02-02551-8.
Media użyte na tej stronie
Autor: Autor nie został podany w rozpoznawalny automatycznie sposób. Założono, że to 4C~commonswiki (w oparciu o szablon praw autorskich)., Licencja: CC-BY-SA-3.0
Illustration of Euler's line in a triangle
Circumcenter of a triangle
The incenter of a triangle
An equilateral triangle.
Triangle with notations for sides and angles..
Autor: Wersję rastrową wykonał użytkownik polskiego projektu wikipedii: Andrut, Zwektoryzował: Krzysztof Zajączkowski, Licencja: CC BY-SA 2.5
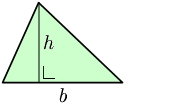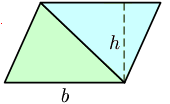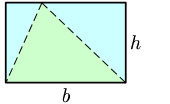
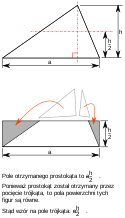
Rysunek ma na celu pomoc w zapamiętaniu i zrozumieniu jednego z podstawowych wzorów na pole trójkąta