Trójkąt Pascala

Trójkąt Pascala – trójkątna tablica liczb:

 0                     1
 1                   1   1
 2                 1   2   1
 3               1   3   3   1
 4             1   4   6   4   1
 5           1   5   10  10   5   1
 6         1   6   15  20  15   6   1
 7       1   7   21  35  35   21  7   1
 8     1   8   28  56  70  56   28  8   1
 9   1   9  36   84  126 126  84  36  9   1
      . . . . . . . . . . . . . . . . . . .

Każda liczba w trójkącie jest sumą dwóch liczb znajdujących się bezpośrednio nad nią

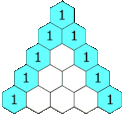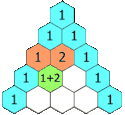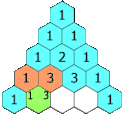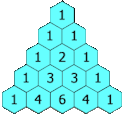
Na bokach trójkąta znajdują się liczby 1, a pozostałe powstają jako suma dwóch bezpośrednio znajdujących się nad nią^[1]. Liczby stojące w n-tym wierszu to kolejne współczynniki dwumianu Newtona – rozwinięcia ${\displaystyle (a+b)^{n}.}$ Na przykład:

• ${\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}}$ w trzecim wierszu trójkąta mamy 1, 3, 3, 1.
• ${\displaystyle (a+b)^{5}=1a^{5}b^{0}+5a^{4}b^{1}+10a^{3}b^{2}+10a^{2}b^{3}+5a^{1}b^{4}+1a^{0}b^{5}}$

Inaczej: licząc miejsca w wierszu i kolumnie od zera, liczba stojąca na miejscu k w wierszu n jest równa ${\displaystyle {n \choose k}.}$

Przykład: W wierszu 5 na miejscu 2 stoi 10 co jest właśnie równe ${\displaystyle {5 \choose 2}.}$

Uważa się, że trójkąt ten został odkryty na przełomie XI i XII w. przez Chińczyków i niezależnie przez Omara Chajjama XI. W XVII w. matematyk francuski Blaise Pascal połączył studia nad prawdopodobieństwem z tym trójkątem, osiągając tak znakomite wyniki, że trójkąt ten nazwany został trójkątem Pascala.

Własności trójkąta

Sumy liczb w poziomych rzędach to kolejne potęgi liczby 2

(c) Nonenmac z angielskiej Wikipedii, CC BY-SA 3.0

Wyróżnione elementy trójkąta Pascala podzielne przez 3

• Na skrajnych bocznych (zerowy) rzędach trójkąta są jedynki.
• W kolejnym (pierwszym) skrajnym bocznym rzędzie są kolejne liczby naturalne (1, 2, 3, 4,...).
• W drugim rzędzie różnice między sąsiednimi liczbami są kolejnymi liczbami naturalnymi (są to liczby trójkątne). Liczby trójkątne podają liczbę okręgów ułożonych w kształt trójkąta (1, 3, 6, 10,...).
• W trzecim liczby piramidalne, podają liczbę kulek ułożonych czworościan foremny (1, 4, 10, 20, 35,...).
• W czwartej liczbę kul w „czworościanie” w przestrzeni czterowymiarowej.
• Uogólniając, w n tym rzędzie bocznym znajdują się liczby n-komórkowe.
• Wracając do rzędu zerowego i uogólniając możemy policzyć liczbę elementów w trójkącie w przestrzeni jedno- i zerowymiarowej.
• Sumy liczb w poziomych rzędach to kolejne potęgi liczby 2.
• Każdy element trójkąta zawiera liczbę różnych dróg, jakimi można do niego dotrzeć z wierzchołka poruszając się do sąsiednich elementów w lewo w dół oraz w prawo w dół.
• Po usunięciu z trójkąta wszystkich liczb parzystych pozostałe liczby nieparzyste układają się w geometryczny wzór trójkąta Sierpińskiego. Podobna prawidłowość zachodzi także dla dowolnych liczb naturalnych:

 0                     1                                      #
 1                   1   1                                  #   #
 2                 1   2   1                              #       #
 3               1   3   3   1                          #   #   #   #
 4             1   4   6   4   1                      #               #
 5           1   5  10  10   5   1                  #   #           #   #
 6         1   6  15  20  15   6   1              #       #       #       #
 7       1   7  21  35  35  21   7   1          #   #   #   #   #   #   #   #
 8     1   8  28  56  70  56   28  8   1      #                               #
 9   1   9  36  84  126 126 84  36   9   1  #   #                           #   #

• Suma kwadratów wszystkich elementów wiersza o numerze n (numerując od zera) jest równa środkowemu elementowi wiersza 2n.

Zastosowania

Biologia

W genetyce w odniesieniu do genów kumulatywnych. Biorąc co drugi wiersz zaczynając od wiersza drugiego (1:2:1) trójkąt pokazuje stosunki rozszczepień w przypadku cech determinowanych przez geny kumulatywne^[2].

Rachunek prawdopodobieństwa i statystyka

Każdy współczynnik obrazuje liczbę dróg, którymi można dojść od wierzchołka do danego punktu – ma to wykorzystanie przy analizie prawdopodobieństwa przy użyciu Deski Galtona^[3].

Programy obliczające

Animacja trójkąta Pascala w reprezentacji binarnej.

Przykład prostej (ale nieekonomicznej) funkcji rekurencyjnej w języku Pascal, obliczającej element trójkąta Pascala. Wzór wynika z definicji rekurencyjnej elementów trójkąta.

${\displaystyle {n \choose 0}={n \choose n}=1.}$

${\displaystyle {n \choose k}={n-1 \choose k-1}+{n-1 \choose k}}$

function pascal(n,k:integer):integer;
begin
  if (k=0) or (k=n) then
     pascal := 1
  else
     pascal := pascal(n-1, k-1) + pascal(n-1,k);
end;

Przykład drzewa Pascala napisany w języku C++, n – liczba wierszy, tablica zwraca wartość współczynnika w zadanym wierszu i kolumnie:

  long long **trojkatPascala;
  trojkatPascala= new long long *[n];
  for (int j=0;j<n;j++)
  {
    trojkatPascala[j]=new long long [j+1];
    trojkatPascala[j][0]=1;
    trojkatPascala[j][j]=1;

    for (int i=0; i<j-1; i++)
      trojkatPascala[j][i+1]=trojkatPascala[j-1][i]+trojkatPascala[j-1][i+1];
  }

A oto przykład programu w Pythonie wypisującego liczby z trójkąta Pascala dla zadanej liczby rzędów:

def write_list(list):
    print(' '.join([str(item) for item in list]).center(30))

x = input("Podaj liczbe poziomow: ")
line = [1]
write_list(line)
for i in range(int(x) - 1):
    next_line = [1]
    for j in range(len(line) - 1):
        next_line.append(line[j] + line[j + 1])
    next_line.append(1)
    line = next_line
    write_list(line)

Zobacz też

• kombinacja
• symbol Newtona

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Pascal's Triangle, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12]  (ang.).
• Praca Pascala Traité du triangle arithmétique z 1654 (po francusku) wraz z opisem w j. angielskim