Trysekcja kąta

Trysekcja kąta – jeden z trzech (obok podwojenia sześcianu i kwadratury koła) wielkich problemów matematyki greckiej. Polega on na podziale kąta na trzy równe części^[1] jedynie przy użyciu cyrkla i liniału. W roku 1837 Pierre Wantzel udowodnił, że konstrukcja taka w ogólnym przypadku jest niewykonalna. Posługując się narzędziami teorii Galois można wykazać, że dla danego kąta ${\displaystyle \varphi }$ kąt o mierze ${\displaystyle {\tfrac {1}{3}}\varphi }$ jest konstruowalny wtedy i tylko wtedy, gdy wielomian

${\displaystyle 4x^{3}-3x-\cos \varphi }$

jest rozkładalny w ciele ${\displaystyle \mathbb {Q} (\cos \varphi ).}$

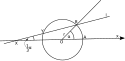
Konstrukcja Archimedesa

Rezygnując z wymogu użycia tylko cyrkla i liniału, można dokonać trysekcji kąta ostrego, wykorzystując konstrukcję Archimedesa (konstrukcja neusis). Używa się do niej cyrkla i liniału z zaznaczonymi dwoma punktami X i Y. Najpierw należy nakreślić okrąg o środku O (gdzie O – wierzchołek kąta) i promieniu ${\displaystyle r=|XY|.}$ Punkty przecięcia okręgu z ramionami kąta oznaczyć jako A i B. Następnie poprowadzić prostą OA oraz prostą ${\displaystyle l}$ za pomocą linijki tak, aby jeden z zaznaczonych na linijce punktów np. X należał do prostej OA, zaś (drugi zaznaczony na linijce punkt) Y należał do okręgu i tak by prosta ${\displaystyle l}$ przechodziła przez punkt B. Wówczas proste OA i ${\displaystyle l}$ przetną się pod kątem ${\displaystyle {\frac {\alpha }{3}}.}$

Przypisy

Bibliografia

• Jerzy Browkin: Teoria ciał. Państwowe Wydawnictwo Naukowe, 1978.
• Agnieszka Nawrot Sabak: Encyklopedia Matematyka. Kraków: GREG, 2008, s. 245. ISBN 978-83-7517-015-3.

Linki zewnętrzne

• (ang.) John J O’Connor, Edmund F. Robertson, Trysekcja kąta w MacTutor History of Mathematics archive