Twierdzenie Kopernika

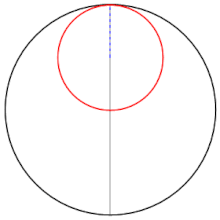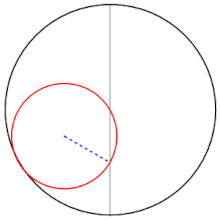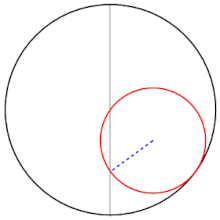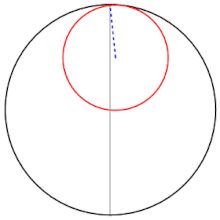
Twierdzenie Kopernika – animacja

Ilustracja twierdzenia Kopernika – XIII-wieczny szkic Nasir al-Dina Tusiego

Twierdzenie Kopernika – twierdzenie geometrii płaskiej; mówi ono, że jeśli wewnątrz okręgu toczy się bez poślizgu okrąg o promieniu dwa razy mniejszym, to dowolny, lecz ustalony punkt małego okręgu porusza się prostoliniowo po średnicy okręgu większego. Innymi słowy hipocykloida, w której mniejszy okrąg jest mniejszy dwukrotnie, jest odcinkiem.

Historia

Twierdzenie to pojawiło się w literaturze co najmniej trzykrotnie:

• około 461 r. n.e. Proklos sformułował je w swoim Komentarzu do pierwszej księgi Elementów Euklidesa^[1];
• następnie w 1254 r. ponownie opublikował je perski astronom i matematyk Nasir ad-Din Tusi^[2] (stąd twierdzenie to jest szerzej znane po angielsku jako Tusi-couple);
• w 1543 r. w dziele De revolutionibus orbium coelestium polskiego polihistora Mikołaja Kopernika. Kopernik sformułował to twierdzenie, prawdopodobnie nie wiedząc, że zostało ono co najmniej dwukrotnie opisane i opublikowane wcześniej.

Zobacz też

• epicykloida

Przypisy

Bibliografia

• Alexander Bogomolny: Copernicus' Theorem (ang.). [dostęp 2008-12-29].