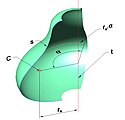
Twierdzenie Pappusa-Guldina

Twierdzenia Pappusa-Guldina, reguły Guldina^[1] – dwa twierdzenia stereometrii, ułatwiające obliczanie pola powierzchni obrotowej oraz objętości bryły obrotowej w oparciu o położenie środka masy obracanej krzywej lub figury.

Twierdzenia nazwane zostały od nazwisk Pappusa z Aleksandrii i Paula Guldina.

Pierwsze twierdzenie Pappusa-Guldina

Pole powierzchni, powstałej przez obrót jednorodnej i płaskiej linii dookoła osi leżącej w płaszczyźnie tej linii i nie przecinającej jej, jest równe długości linii ${\displaystyle (s)}$ pomnożonej przez długość okręgu ${\displaystyle (l=2\pi r_{s})}$ opisanego przy obrocie przez jej środek masy (punkt ${\displaystyle C}$).

Np. dla torusa o promieniu ${\displaystyle R}$ i promieniu okręgu ${\displaystyle r,}$ długość linii ${\displaystyle s=2\pi r,}$ długość okręgu dla środka masy ${\displaystyle l=2\pi R,}$ stąd pole torusa ${\displaystyle s\cdot l=4\pi ^{2}rR.}$

Drugie twierdzenie Pappusa-Guldina

Objętość bryły, powstałej przy obrocie figury płaskiej dookoła osi leżącej w płaszczyźnie tej figury i nie przecinającej jej, jest równa polu powierzchni figury ${\displaystyle (A)}$ pomnożonemu przez długość okręgu opisanego ${\displaystyle (l=2\pi R_{s})}$ przy obrocie przez jej środek ciężkości (punkt ${\displaystyle C_{A}}$).

Np. dla torusa o promieniu ${\displaystyle R}$ i promieniu koła ${\displaystyle r,}$ pole powierzchni koła ${\displaystyle A=\pi r^{2},}$ długość okręgu dla środka masy ${\displaystyle l=2\pi R,}$ stąd objętość torusa ${\displaystyle A\cdot l=2\pi ^{2}r^{2}R.}$

Zobacz też

• twierdzenie Pappusa

Przypisy

Linki zewnętrzne

• Marek Kordos, O obrotach figur płaskich. „Delta”, listopad 2015. [dostęp 2016-09-03]..
• Eric W.E.W. Weisstein Eric W.E.W., Pappus's Centroid Theorem, [w:] MathWorld [online], Wolfram Research  (ang.). [dostęp 2022-06-20].