Twierdzenie transportu Reynoldsa

Ten artykuł od 2018-03 wymaga zweryfikowania podanych informacji. Należy podać wiarygodne źródła, najlepiej w formie przypisów bibliograficznych. Część lub nawet wszystkie informacje w artykule mogą być nieprawdziwe. Jako pozbawione źródeł mogą zostać zakwestionowane i usunięte. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Przepływ przez objętość kontrolną

Twierdzenie transportu Reynoldsa – jedno z kluczowych twierdzeń w dynamice płynów. Umożliwia sformułowanie podstawowych praw wykorzystywanych w dynamice płynów – równania zachowania masy, drugiej zasady dynamiki Newtona oraz praw termodynamiki.

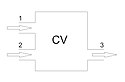
Sens twierdzenia transportu Reynoldsa można wyjaśnić, zakładając układ, w skład którego wchodzi objętość kontrolna CV (patrz rysunek obok) oraz powierzchnia kontrolną CS, przez którą przepływa płyn. Twierdzenie Reynoldsa stwierdza, że:

Szybkość zmian ekstensywnej wartości B w układzie jest równa szybkości zmian ilości tej wartości w objętości kontrolnej oraz zmianie szybkości przepływu tej wartości przez powierzchnię kontrolną.

Przykładem wartości ekstensywnej występującej w równaniu jest masa. Prawo zachowania masy stwierdza, że szybkość przyrostu (bądź spadku) masy jest równa akumulacji masy w objętości kontrolnej oraz różnicy prędkości przepływu przez powierzchnię kontrolną.

Twierdzenie to można zapisać matematycznie w postaci równania:

${\displaystyle {\frac {(dB)}{dt}}={\frac {d}{dt}}\int \limits _{CV}b\rho d\upsilon +\int \limits _{CS}b\rho (V\cdot n)dA}$

lub

${\displaystyle {\frac {(dB)}{dt}}=\int \limits _{CV}{\frac {\partial }{\partial t}}b\rho d\upsilon +\int \limits _{CS}b\rho (V\cdot n)dA,}$

gdzie:

${\displaystyle B}$ – wartość ekstensywna,

${\displaystyle b}$ – wartość intensywna,

${\displaystyle \rho }$ – gęstość,

${\displaystyle \upsilon }$ – objętość,

${\displaystyle V}$ – prędkość przepływu,

${\displaystyle n}$ – wektor jednostkowy normalny powierzchni kontrolnej.

Postać różniczkowa tego równania z dodatkowymi założeniami nosi nazwę równania Naviera-Stokesa.

Zastosowanie w inżynierii

Stała objętość kontrolna

Ponieważ twierdzenie Reynoldsa odgrywa kluczową rolę w dynamice płynów, znajduje szerokie zastosowanie w inżynierii chemicznej oraz innych gałęziach inżynierii, w których spotkać można zagadnienia związane z przepływami płynów. Jeżeli przyjmie się pewne założenia, równanie można przekształcać i upraszczać do postaci, które można łatwo wykorzystać.

Przykładem jest bilans masy. Za wartość ekstensywną przyjmijmy masę ${\displaystyle (B=m){:}}$

${\displaystyle b={\frac {dB}{dm}}={\frac {dm}{dm}}=1.}$

Otrzymujemy:

${\displaystyle {\frac {(dB)}{dt}}={\frac {d}{dt}}\int \limits _{CV}\rho d\upsilon +\int \limits _{CS}\rho (V\cdot n)dA,}$

zakładając przepływ ustalony (dm/dt = 0) otrzymujemy:

${\displaystyle 0={\frac {d}{dt}}\int \limits _{CV}\rho d\upsilon +\int \limits _{CS}\rho (V\cdot n)dA,}$

jeżeli założymy, że gęstość jest stała (${\displaystyle \partial \rho }$/${\displaystyle \partial t=0}$) równanie przybierze postać:

${\displaystyle 0=\int \limits _{CS}\rho (V\cdot n)dA,}$

zakładamy przepływ jest jednokierunkowy:

${\displaystyle 0=\int \limits _{CS}\rho VdA,}$

co można zapisać:

${\displaystyle \sum _{i}\left(\rho _{i}\cdot V_{i}\cdot A_{i}\right)=0}$ lub ${\displaystyle \sum _{i}{\dot {m}}_{i}=0,}$

gdzie ${\displaystyle {\dot {m}}}$ przepływ masowy wyrażony w jednostce masy na jednostkę czasu.

Dla przypadku przedstawionego na rysunku obok równanie to przybierze prostą postać:

${\displaystyle \rho _{3}\cdot V_{3}\cdot A_{3}=\rho _{1}\cdot V_{1}\cdot A_{1}+\rho _{2}\cdot V_{2}\cdot A_{2}.}$

Jeżeli ${\displaystyle \rho =idem}$

${\displaystyle V_{3}\cdot A_{3}=V_{1}\cdot A_{1}+V_{2}\cdot A_{2}}$ (równanie ciągłości strugi).

Zachowanie masy

Przyjmując za wartość ekstensywną masę, równanie przybiera postać:

${\displaystyle 0={\frac {d}{dt}}\int \limits _{CV}\rho d\upsilon +\int \limits _{CS}\rho (V\cdot n)dA.}$

Zachowanie energii

Jeżeli za wartość ekstensywną przyjmiemy energię, to równanie przyjmie postać:

${\displaystyle E={\dot {Q}}-\sum {}{\dot {W}}={\frac {d}{dt}}\int \limits _{CV}e\cdot \rho d\upsilon +\int \limits _{CS}e\cdot \rho (V\cdot n)dA.}$

Jeżeli uwzględnimy wszystkie rodzaje energii (kinetyczną, wewnętrzną, potencjalną i inne) i podstawimy te wyrażenia za ${\displaystyle e}$ otrzymamy postać równania:

${\displaystyle E={\dot {Q}}-\sum {}{\dot {W}}={\frac {d}{dt}}\int \limits _{CV}\rho \left({\frac {V^{2}}{2}}+gz+{\tilde {u}}\right)d\upsilon +\int \limits _{CS}\left({\frac {V^{2}}{2}}+gz+{\tilde {u}}\right)\rho (V\cdot n)dA,}$

gdzie:

${\displaystyle Q}$ – ilość ciepła oddana do układu,

${\displaystyle W}$ – praca wykonana przez układ.

Zachowanie pędu

W przypadku gdy za wartość ekstensywną przyjmiemy pęd wartość b (intensywna) staje się prędkością, natomiast lewa strona równania (zgodnie z drugą zasadą dynamiki Newtona) przyjmuje wartość siły. Równanie można zapisać jako:

${\displaystyle {\frac {d}{dt}}(mV)=\sum _{i}F_{i}={\frac {d}{dt}}\int \limits _{CV}V\rho d\upsilon +\int \limits _{CS}V\rho (V\cdot n)dA.}$

Zobacz też

• dynamika płynów
• prawa zachowania