Wahadło Foucaulta

Wahadło Foucaulta w Panteonie w Paryżu

Wahadło Foucaulta w Centrum Nauki Kopernik w Warszawie

Wahadło Foucaulta – wahadło mające możliwość wahań w dowolnej płaszczyźnie pionowej^[1]. Powolna zmiana płaszczyzny ruchu wahadła względem Ziemi dowodzi jej obrotu wokół własnej osi. Nazwa wahadła upamiętnia jego wynalazcę, Jeana Bernarda Léona Foucaulta, który zademonstrował je w lutym 1851 roku w Paryskim Obserwatorium Astronomicznym. Kilka tygodni później eksperyment powtórzono w Panteonie w Paryżu.

Działanie

Animacja ruchu wahadła na półkuli południowej. Obrót płaszczyzny drgań przesadzony.

Jeżeli wahadło zostanie wprawione w ruch, to obserwator na Ziemi zauważy, że płaszczyzna wahań wolno zmieniła się. Gdyby wahadło umieścić na biegunie geograficznym Ziemi i puścić je tak by w układzie odniesienia względem gwiazd poruszało się w płaszczyźnie zawierającej oś obrotu Ziemi, to zawieszenie wahadła (umieszczone na osi obrotu Ziemi) nie zmieni płaszczyzny drgań wahadła, dlatego w ciągu doby (gwiazdowej) płaszczyzna jego wahań obróci się względem obserwatora na Ziemi o 360°^[2].

Na mniejszych szerokościach geograficznych obrót będzie odpowiednio wolniejszy. Szybkość obrotu płaszczyzny wahań zależy od szerokości geograficznej φ i wynosi:

15°·sin(φ) na godzinę.

Wahadło Foucaulta w Muzeum Sztuk i Rzemiosł w Paryżu; w miarę obrotu wahadło przewraca ustawione wokoło klocki.

Wahadło Foucaulta w budynku Wydziału Fizyki Uniwersytetu im. Adama Mickiewicza w Poznaniu

Historia

Przed Foucaultem zmianę płaszczyzny drgań wahadła zaobserwował w 1660 lub 1661 roku Vincenzo Viviani, ale nie powiązał tego z ruchem obrotowym Ziemi^[3]. Według relacji Foucaulta, pierwszej próby obserwacji zmian płaszczyzny drgań wahadła o długości 2 m i masie około 5 kg dokonał on 8 stycznia 1851 roku (być może 6, 7 lub 8) o godzinie 2 w nocy w piwnicy swojego domu. 3 lutego zorganizował pokaz dla zaproszonych gości z 11 metrowym wahadłem w paryskim obserwatorium astronomicznym. Dzięki wsparciu prezydenta Francji Ludwika Napoleona zorganizował 31 marca 1851 roku publiczną prezentację w Panteonie. Na stalowym drucie zawieszony został mosiężny obciążnik o masie 28 kg, wahadło miało długość 67 m (220 stóp, 62 funty)^[4]. Ten wielokrotnie powtarzany pokaz przyciągał tłumy i wywołał manię wahadła w Europie i Stanach Zjednoczonych^[5].

Założenia

Wahadło Foucaulta rozpatruje się jako wahadło matematyczne zaburzane przez siłę wywołaną obrotem punktu zawieszenia wahadła. Dla uproszczenia zakłada się, że amplituda drgań jest na tyle mała, aby dla siły zaburzającej uznać, że oscylująca masa wahadła przesuwa się poziomo. Przyjmuje się układ współrzędnych, w którym punkt O jest punktem równowagi wahadła, płaszczyzna Oxy jest pozioma, oś Ox skierowana na wschód a Oy w na północ. Trzecia oś Oh jest pionowa i skierowana do góry.

Wahadło matematyczne

W przypadku małych wychyleń i pomijając obrót Ziemi względem inercjalnego układu odniesienia, równania ruchu wahadła matematycznego określone są przez:

${\displaystyle {\begin{cases}{\ddot {x}}=-\omega ^{2}x\\{\ddot {y}}=-\omega ^{2}y\end{cases}},}$

${\displaystyle \omega ={\sqrt {g/l}},}$

gdzie:

ω – częstość kołowa wahadła matematycznego,

g – przyspieszenie ziemskie,

l – długość wahadła.

Zakładając, że w czasie t = 0, wahadło przechodzi przez O z prędkością V₀ wzdłuż osi Ox, wówczas rozwiązanie można przedstawić jako:

${\displaystyle {\begin{aligned}x&={\frac {V_{0}}{\omega }}\sin(\omega t),\\y&=0.\end{aligned}}}$

Wahadło takie porusza się w niezmieniającej swego położenia płaszczyźnie.

Równania ruchu wahadła Foucaulta

Ciało poruszające się względem Ziemi, z powodu jej obrotu względem inercjalnego układu odniesienia, doznaje przyspieszenia Coriolisa. Dla ciała poruszającego się poziomo, oraz pomijając przyspieszenia działające w kierunku pionowym, równania ruchu wahadła przyjmują postać:

${\displaystyle {\begin{cases}{\ddot {x}}=-\omega ^{2}x+2{\dot {y}}\Omega \sin {\theta },\\{\ddot {y}}=-\omega ^{2}y-2{\dot {x}}\Omega \sin {\theta }.\end{cases}}}$

Przyjęto układ współrzędnych związany z danym położeniem na powierzchni Ziemi: oś x-ów wskazuje kierunek wschodni, oś y-ów wskazuje kierunek północny.

Używając liczb zespolonych i przyjmując ${\displaystyle z=x+iy,}$ powyższe można wyrazić wzorem:

${\displaystyle {\ddot {z}}+2i\Omega \sin {\theta }{\dot {z}}+\omega ^{2}z=0,}$

gdzie:

${\displaystyle \Omega }$ – częstość kołowa obrotu Ziemi wokół własnej osi,

${\displaystyle \theta }$ – szerokość geograficzna.

Częstość kołowa Ω związana jest z czasem T obrotu Ziemi wokół własnej osi, czyli dobą gwiazdową równą 23 godziny 56 minut i 4 sekundy = 86164 sekund:

${\displaystyle \Omega ={\frac {2\pi }{T}}=0{,}0000729s^{-1}.}$

Zakładając, że rozwiązania przyjmują postać ${\displaystyle z(t)=e^{rt},}$ zespolone ${\displaystyle r}$ spełnia równanie kwadratowe: ${\displaystyle r^{2}+2i\Omega \sin(\theta )r+\omega ^{2}=0}$ co można wyrazić jako: ${\displaystyle \left(r+i\Omega \sin(\theta )\right)^{2}-i^{2}\omega ^{2}\left(1+\sin ^{2}(\theta ){\frac {\Omega ^{2}}{\omega ^{2}}}\right)=0.}$

Przyjmując ${\displaystyle \omega _{0}={\sqrt {\omega ^{2}+\Omega ^{2}\sin ^{2}(\theta )}},}$ powyższe równanie ma dwa rozwiązania: ${\displaystyle r=-i(\Omega \sin(\theta )\pm \omega _{0}).}$ Ogólne rozwiązanie układu ma postać:

${\displaystyle z(t)=e^{-i\Omega \sin {\theta }t}\left(c_{1}e^{i\omega _{0}t}+c_{2}e^{-i\omega _{0}t}\right),}$

gdzie:

• ${\displaystyle c_{1}}$ i ${\displaystyle c_{2}}$ – dwie stałe zespolone, dobierane tak by rozwiązanie spełniało warunki na położenie i prędkość w chwili t = 0, prowadzą one do dwóch równań:

${\displaystyle {\begin{cases}z(0)=c_{1}+c_{2},\\{\dot {z}}(0)=-i\left(\Omega \sin(\theta )z(0)-\omega _{0}(c_{1}-c_{2})\right).\end{cases}}}$

Podstawiając wyrażenia określające stałe do równania, otrzymuje się:

${\displaystyle z(t)=e^{-i\Omega \sin {\theta }t}\left[z_{0}\left(\cos(\omega _{0}t)+i{\frac {\Omega \sin(\theta )}{\omega _{0}}}\sin(\omega _{0}t)\right)+{\frac {{\dot {z}}_{0}}{\omega _{0}}}\sin(\omega _{0}t)\right].}$

Wyrażenie to jest iloczynem, w którym pierwszy czynnik zmienia się wolno (${\displaystyle \Omega \sin {\theta }\ll \omega _{0}}$). Czynnik w nawiasie jest sumą szybkozmiennych funkcji trygonometrycznych (duże ${\displaystyle \omega _{0}}$). Składniki w nawiasie zawierają zarówno część rzeczywistą, jak i urojoną, w ogólności są równaniem elipsy o parametrach zależnych od ${\displaystyle z_{0},}$ ${\displaystyle {\dot {z}}_{0}}$ i ${\displaystyle \Omega \sin(\theta )/\omega _{0}.}$ Z czego wynika, że wahadło Foucaulta porusza się po elipsie z częstością ω₀, obracającą się wolno w przestrzeni. Zmiana płaszczyzny drgań zachodzi z częstością:

${\displaystyle \omega _{f}=\Omega \sin(\theta ).}$

Czas jednego obrotu płaszczyzny wahań wahadła wynosi:

${\displaystyle T_{f}={\frac {2\pi }{\Omega \sin(\theta )}}={\frac {T}{\sin(\theta )}}.}$

Czas jednego pełnego obrotu wahadła w danym miejscu na Ziemi zwany jest dobą wahadła (pendulum day), jest on jednakowy dla wszystkich punktów leżących na tej samej szerokości geograficznej. Najkrótsza doba wahadła jest na biegunie i jest równa dobie gwiazdowej, na szerokości geograficznej 30° jest dwukrotnie większa i dąży do nieskończoności przy zbliżaniu się do równika.

Z zależności na ruch wahadła wynika, że każde wahadło mające swobodę zmiany płaszczyzny drgań poruszające się na Ziemi (poza równikiem) zmienia płaszczyznę drgań. Zmiana ta jest zależna jedynie od szerokości geograficznej, nie zależy od długości wahadła, jego amplitudy, masy itp. Jednak zależności zostały wyprowadzone z przyjęciem wielu uproszczeń, oznacza to że w rzeczywistości płaszczyzna drgań wahadła może zależeć od innych czynników, które z powodu przyjętych uproszczeń nie wystąpiły w końcowych zależnościach.

Szczególne przypadki ruchu wahadła

Wahadło wypchnięte z położenia równowagi

Najłatwiej rozważyć przypadek gdy wahadło w czasie t = 0, przechodzi przez położenie równowagi (${\displaystyle z(0)=0,}$ ${\displaystyle {\dot {z}}(0)=V_{0}}$) wówczas równanie ruchu wahadła upraszcza się do:

${\displaystyle z(t)={\frac {V_{0}}{\omega _{0}}}e^{-i\Omega \sin(\theta )t}\sin(\omega _{0}t).}$

Drugi czynnik (sinus) odpowiada za pulsację wahadła tak jak w wahadle matematycznym, wahadło cyklicznie powraca do stanu równowagi. Pierwszy czynnik odpowiada za obrót płaszczyzny drgań, ale wpływa też on na kształt toru ruchu, który odchyla się od płaszczyzny drgań wahadła matematycznego, przyjmując kształt rozety (patrz animacja powyżej). Ten rodzaj ruchu wydaje się najprostszą realizacją ruchu wahadła Foucaulta, ale jest on trudny do realizacji, gdyż nie ma prostego sposobu na wprawienie w ruch wahadła, tak by przeszło dokładnie przez położenie równowagi.

Wahadło wychylone i puszczone

Wykres symulacji toru ruchu wahadła wychylonego i puszczonego. Długość wahadła 67 m, szerokość geograficzna 48°52′, wychylenie 6 m. Oś odchylenia skalowana w mm.

Innym sposobem uruchomienia wahadła, jest wychylenie go z położenia równowagi (${\displaystyle z_{0}\neq 0,}$ ${\displaystyle {\dot {z}}_{0}=0}$) i swobodne puszczenie. Wówczas tor ruchu wahadła opisuje zależność:

${\displaystyle z(t)=z_{0}e^{-i\Omega \sin(\theta )t}\left[\cos(\omega _{0}t)+i{\frac {\Omega \sin(\theta )}{\omega _{0}}}\sin(\omega _{0}t)\right].}$

W przeciwieństwie do poprzedniego przypadku, teraz wahadło nie przechodzi przez punkt równowagi, ale porusza się po elipsie, która powoli obraca się. Pomijając zmianę pierwszego czynnika w trakcie jednego wahnięcia wahadła, półosie elipsy określają wyrażenia:

${\displaystyle a=z_{0},}$

${\displaystyle b=z_{0}{\frac {\Omega \sin(\theta )}{\omega _{0}}}\approx z_{0}\Omega \sin(\theta ){\sqrt {\frac {l}{g}}}.}$

Obserwator patrzący na wahadło poruszające się na półkuli północnej widzi, że mija ono punkt równowagi z prawej strony, na półkuli południowej z lewej.

Wahadło na Panteonie w Paryżu

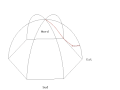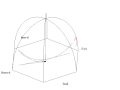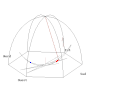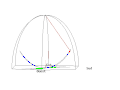
Pierwsze zademonstrowane szerokiej publiczności wahadło uruchomiono w lutym 1851 roku w Panteonie w Paryżu, miało ono długość 67 m, okres drgań takiego wahadła wynosi 16,42 sekundy. Wahadło zostało wychylone o około 6 m z położenia równowagi przywiązane nicią podtrzymującą je, następnie przepalono nić. Płaszczyzna drgań wahadła umieszczonego na szerokości geograficznej Panteonu w Paryżu (48°52′) obraca się w ciągu godziny o:

${\displaystyle -\Omega \sin(48^{\circ }52')\times {\frac {360^{\circ }}{2\pi }}\times 3600=-11^{\circ }19'.}$

Elipsa wahadła o tych parametrach ma półosie:

• duża – 6 m,
• mała – 0,84 mm.

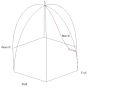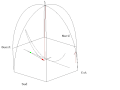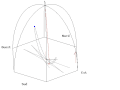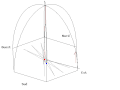
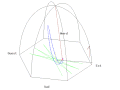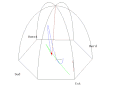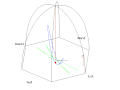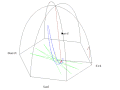
Poniższe animacje przedstawiają symulację drgań wahadła w Panteonie w Paryżu, czas animacji odpowiada 1/4 doby. W celu lepszego zobrazowania jego ruchu zmieniono parametry ruchu. Wahadło startuje wychylone 50 m na wschód z położenia równowagi, Ziemia obraca się tak jakby doba trwała 110 s. W środku animacji umieszczono słupek, który rzuca cień Słońca.

• Animacje wahadła Foucaulta w Panteonie w Paryżu
• 

  Obserwator spoczywa względem Ziemi

• 

  Obserwator spoczywa w płaszczyźnie drgań wahadła

• 

  Obserwator spoczywa względem Słońca

Zaburzenia ruchu wahadła

Na wahadło mogą wpływać czynniki zewnętrzne zaburzające pracę wahadła, wpływają też czynniki wewnętrzne, które zostały pominięte. Rozważane jest wiele czynników, wśród nich: asymetria wahadła, tłumienie, nieliniowość wahadła związana z amplitudą. Wpływ czynników można rozważać jako wpływ na parametry elipsy wahadła^[6].

Zaburzenie może zmieniać prędkość obrotu płaszczyzny drgań w przestrzeni, które można wyrazić przez częstość kołową, która zmniejsza lub zwiększa częstość obrotu płaszczyzny drgań wywołanej obrotem zawieszenia wahadła. Oraz kształt elipsy, który można wyrazić przez stosunek osi elipsy:

${\displaystyle \omega =\omega _{f}+\omega _{z}}$ – częstość obrotu wahadła z zaburzeniem,

${\displaystyle \epsilon ={\frac {b}{a}}}$ – definicja wydłużenia elipsy,

Precesja wahadła sferycznego

Rozważanie wahadła Foucaulta jako wahadła matematycznego jest uproszczeniem. Układ zawieszenia wahadła musi zapewnić możliwość obrotu płaszczyzny drgań wahadła, przez co wahadło takie jest wahadłem sferycznym. Ruch wahadła sferycznego można przybliżyć elipsą. Elipsa ta obraca się (precesja Airy) z prędkością kątową^[7]:

${\displaystyle \omega _{pr}={\frac {3A}{4l^{2}T}}={\frac {3}{8}}{\frac {ab}{l^{2}}}\omega _{w}={\frac {3}{8}}{\frac {ab}{g^{2}}}\omega _{w}^{5}={\frac {3}{8}}{\frac {S}{\pi g^{2}}}\omega _{w}^{5},}$

gdzie:

a, b – półosie elipsy,

g – przyspieszenie ziemskie,

S – pole elipsy,

ω_w – częstość kołowa wahadła.

Dla krótkiego, nawet precyzyjnie uruchomionego, wahadła precesja ta może przekroczyć precesję Foucalta.

Tłumienie precesji wahadła. Pierścień Charrona

Wahadło idealnie wychylone i puszczone w najdalszym punkcie wychylenia spoczywa względem powierzchni Ziemi. Wahadło zaburzone poruszające się po elipsie najdalszym od równowagi punkcie toru porusza się kierunku prostopadłym do płaszczyzny drgań. Tłumienie tego ruchu usunie ruch zaburzający obrót płaszczyzny wahań. Jedną z metod zwaną pierścieniem Charrona opracował w 1931 roku Fernand Charron. W pobliżu punktu zawieszenia (zazwyczaj) wahadła umieszcza się pierścień, przez który przechodzi drut na którym wisi wahadło. Średnicę pierścienia dobiera się tak by przy wychyleniu wahadła drut dotykał do pierścienia. Jeżeli wahadło ma prędkość poprzeczną, to drut przesuwa się względem pierścienia, a w wyniku tarcia tłumiona jest składowa poprzeczna prędkości ruchu wahadła. System jest prosty w wykonaniu i dobrze tłumi ruch poprzeczny wahadła^[8][9][10].

Wpływ amplitudy drgań

Wzrost amplitudy drgań sprawia, tor zakrzywia się w kierunku pionowym, co zmniejsza składową poziomą prędkości, tym samym zmniejszając siłę Coriolisa, dodatkowo wahadło przestaje być harmoniczne, efekty te skutkują zmniejszeniem prędkości obrotu płaszczyzny drgań wahadła^[6]. Dwa pierwsze wyrazy zależności częstości obrotu płaszczyzny drgań od amplitudy opisuje wzór: Wahadło w pobliżu powierzchni Ziemi obraca się z częstością:

${\displaystyle \omega _{fa}=\omega _{f}\left(1-{\frac {3}{8}}{\left({\frac {a}{l}}\right)}^{2}\right),}$

gdzie:

${\displaystyle \omega _{fa}}$ – częstość obrotu wahadła dla dużej amplitudy,

${\displaystyle \omega _{f}}$ – częstość obrotu wahadła dla małej amplitudy,

${\displaystyle a}$ – amplituda drgań wahadła,

${\displaystyle l}$ – długość wahadła.

Wahadło w Palais de la découverte w Paryżu, poniżej cewka magnetyczna układu napędzajacego.

Warunki realizacji

By zaobserwować zmianę płaszczyzny wahań wymagany jest długi czas wahań, dlatego należy zapewnić małe tłumienie i mały wpływ ruchu powietrza na wahadło, osiąga się to poprzez długie ramię wahadła (nawet kilkunastometrowe) duży ciężar wahadła – pozwala to na ruch bez wyraźnego wpływu tłumienia. Na ruch wahadła może wpłynąć asymetria wahadła, jak i ruch powietrza w pomieszczeniu.

Tradycyjne wahadło działa bez napędu, uruchamiane jest i działa przez pewien czas. Wahadła pokazowe są napędzane, takie wahadła mogą być krótsze i mogą działać dowolnie długo. Stosuje się napęd elektromagnetyczny dolny działający na obciążnik wahadła, oraz górny działający w systemie zawieszenia wahadła^[11]. W napędzie dolnym pod wahadłem umieszcza się cewkę. W prostym rozwiązaniu pierścień Charrona włącza cewkę gdy wahadło jest wychylone. Indukcyjność cewki sprawia, że po włączaniu prąd narasta wolno i płynie aż do rozłączania. W wyniku tego w czasie oddalania się wahadła od położenia równowagi jest ono słabiej przyciągane do położenia równowagi niż podczas powrotu wahadła. W innych rozwiązaniach pod wahadłem umieszcza się układ rozpoznający przejście wahadła przez położenie równowagi^[12].

Wahadła Foucaulta na świecie

Wahadła Foucaulta można spotkać w licznych miejscach na świecie (a zwłaszcza w USA). Ze względu na ich spektakularne wymiary i imponujący wygląd umieszcza się je w miejscach ważnych dla nauki, kultury i polityki (takich jak uniwersytety, muzea, centra kongresowe). Poniższa tabela zawiera największe, najcięższe i najsłynniejsze z nich (w większości przypadków długość wahadeł L została zaokrąglona do pełnych metrów, a masa M do pełnych kilogramów):

Wahadła Foucaulta w Polsce

Wahadło Foucaulta w wieży Zamku Książąt Pomorskich w Szczecinie.

O tym, że Ziemia obraca się wokół swojej osi, możemy się przekonać także w Polsce. W Krakowie, co czwartek odbywają się demonstracje najdłuższego w Polsce wahadła w Kościele św. św. Piotra i Pawła.

Na podstawie znajomości położenia miejsca umocowania wahadła można za pomocą wzoru wyznaczyć częstość oraz okres pozornego obrotu płaszczyzny drgań. Przykładowe dane zostały zamieszczone w tabeli.

W 2013 roku Wahadło Foucaulta zamontowano w Centrum Nowoczesności Młyn Wiedzy w Toruniu. Jest ono przewieszone przez wszystkie osiem kondygnacji budynku, długość liny wynosi 33 m^[20]. Według zamierzeń inwestora miało ono być najdłuższym stale działającym wahadłem Foucaulta w Polsce; dłuższe od niego wahadło w krakowskim kościele św. Piotra i Pawła uruchamiane jest tylko raz w tygodniu, w czwartki^[21].

Zobacz też

• 10 najpiękniejszych eksperymentów z fizyki – wahadło Foucaulta
• kompas żyroskopowy
• żyroskop

Przypisy

Linki zewnętrzne

• Jak eksperymentowano dawniej – Wahadło Foucault’a – sfabularyzowana prezentacja wahadła Foucaulta w Uniwersytecie Mikołaja Kopernika
• The Foucault Pendulum – opis z poglądową animacją, przedstawiającą ruch wahadła w Uniwersytecie Nowej Południowej Walii w Australii (University of New South Wales) (ang.)
• Urwane wahadło Foucaulta – uszkodzenie najsłynniejszego wahadła w paryskim Musée des Arts et Métiers, wyborcza.pl