Warstwa (teoria grup)

Warstwa – podzbiór danej grupy będący jednym z równolicznych elementów jej podziału wyznaczonego przez ustaloną podgrupę, czyli klasa równoważności pewnej relacji równoważności związanej ze wspomnianą podgrupą; jako klasy ustalonej równoważności są one rozłączne, niepuste i wyczerpują całą grupę^[a].

Każda podgrupa wyznacza dwie relacje równoważności o tej samej liczbie warstw – liczbę tę nazywa się indeksem tej podgrupy względem danej grupy^[b]; elementy jednego podziału nazywa się warstwami lewostronnymi, zaś drugiego – prawostronnymi, co ma swoje źródło w charakteryzacji tych zbiorów (zob. Definicja i Własności). Jeżeli obie wspomniane relacje równoważności wprowadzają ten sam podział, to podgrupę wyznaczającą te relacje (ten podział) nazywa się podgrupą normalną.

Pojęcie warstwy umożliwia więc algebraiczną charakteryzację klas tych relacji równoważności, które wprowadzają w grupie podział respektujący jej strukturę; przy założeniu normalności podgrupy wyznaczającej podział zbioru elementów grupy, można na nim (tj. zbiorze ilorazowym) określić strukturę grupy nazywanej grupą ilorazową (zob. Normalność).

Motywacja

Graf przedstawia funkcję, która wprowadza podział w zbiorze ${\displaystyle X,}$ mianowicie dzieli ona dziedzinę na dwa zbiory ${\displaystyle \{1,2\}}$ oraz ${\displaystyle \{3\}}$ będące włóknami odpowiednio nad elementami ${\displaystyle d,c\in Y}$ tworzącymi obraz zbioru ${\displaystyle X,}$ który można utożsamiać z rzutem kanonicznym ${\displaystyle {\overline {X}}}$ wprowadzanej relacji równoważności. Uwaga: włókna mogą mieć dowolną, niezerową liczbę elementów; analogiczna konstrukcja dla grup wymusza, by włókna (warstwy) były równoliczne.

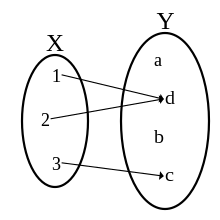
Podział zbioru ${\displaystyle S}$ można przeprowadzić, określając na nim relację równoważności ${\displaystyle \sim ,}$ która podzieli go na rozłączne, niepuste i sumujące się do ${\displaystyle S}$ klasy o wskazanej przez ${\displaystyle \sim }$ własności. Każdą relację ${\displaystyle \sim }$ na ${\displaystyle S}$ można z kolei wprowadzić za pomocą pewnej funkcji ${\displaystyle f\colon S\to S';}$ dwa elementy ${\displaystyle x,y\in S}$ pozostają ze sobą w relacji ${\displaystyle \sim }$ wtedy i tylko wtedy, gdy ich obrazy w funkcji ${\displaystyle f}$ są równe,

${\displaystyle x\sim y\Leftrightarrow f(x)=f(y);}$

mówi się też wtedy, że ${\displaystyle x,y}$ należą do jądra ${\displaystyle \ker f}$ funkcji ${\displaystyle f.}$

Innymi słowy utożsamiane są te elementy dziedziny, które w obrazie przekształcane są na ten sam element ${\displaystyle s'\in S';}$ zbiór tych elementów dziedziny, czyli ${\displaystyle f^{-1}[s']}$ nazywa się włóknem bądź poziomicą albo warstwicą nad ${\displaystyle s'.}$ Obraz ${\displaystyle f[S]\subseteq S'}$ można z kolei utożsamiać ze zbiorem ${\displaystyle {\overline {S}}}$ klas równoważności ${\displaystyle \sim ,}$ czyli funkcja ${\displaystyle S\to f[S]}$ wyznacza i jest wyznaczana przez odwzorowanie ilorazowe ${\displaystyle S\to {\overline {S}}.}$

Powyższe obserwacje można zastosować do homomorfizmu grup ${\displaystyle \varphi \colon G\to G',}$ którego kluczową cechą jest to, że przekształca on nie tylko zbiór ${\displaystyle G}$ w ${\displaystyle G',}$ ale całą grupę ${\displaystyle G}$ w grupę ${\displaystyle G',}$ czyli oprócz ich nośników przenosi (w takim zakresie, w jakim jest to możliwe) również działanie grupowe ${\displaystyle G}$ do ${\displaystyle G'.}$ W tym przypadku jądro ${\displaystyle H=\ker \varphi }$ jest podgrupą w ${\displaystyle G}$^[c]. Otrzymuje się wtedy relację równoważności (podział) w ${\displaystyle G,}$ której charakterystyczną własnością jest to, iż ${\displaystyle H}$ jest jedną z jej klas równoważności; w ogólności są one postaci ${\displaystyle aH=\{ah\colon h\in H\}}$ dla ${\displaystyle a\in G}$^[d][e], a ponadto są równoliczne (zob. Własności, por. rysunek obok). Bezpośrednio stąd wynika, tak jak w opisanym wyżej przypadku teoriomnogościowym, że elementy ${\displaystyle \varphi (a)}$ odpowiadają wprost warstwom ${\displaystyle a(\ker \varphi )}$^[f], tzn. obraz ${\displaystyle \varphi [G]}$ można utożsamiać ze zbiorem ${\displaystyle {\overline {G}}}$ warstw grupy ${\displaystyle G}$ względem ${\displaystyle H}$^[g].

Podział grupy na warstwy względem podgrupy jest więc pojęciem węższym, a przede wszystkim algebraicznie bardziej użytecznym, od dowolnego podziału (zbioru elementów) grupy – tego rodzaju konstrukcję nazywa się kongruencją (przystawaniem). W ogólności przyjmuje się, że ${\displaystyle H}$ może być dowolną podgrupą w ${\displaystyle G,}$ co sprawia, że wyznacza ona dwie, potencjalnie różne relacje równoważności; podgrupa wyznacza jeden podział wtedy i tylko wtedy, gdy jest jądrem homomorfizmu^[h] – do tego zaś potrzeba, a zarazem wystarcza, by była ona normalna (zob. osobna sekcja).

Definicja

Niech ${\displaystyle G}$ będzie dowolną grupą, ${\displaystyle H}$ jej dowolną podgrupą. Podzbiory grupy ${\displaystyle G}$ dane jako

${\displaystyle aH=\{ah\colon h\in H\}\quad {\text{ oraz }}\quad Ha=\{ha\colon h\in H\}}$

dla ${\displaystyle a\in G}$ nazywa się odpowiednio warstwami lewostronną i prawostronną grupy ${\displaystyle G}$ względem ${\displaystyle H}$ wyznaczonymi przez element ${\displaystyle a;}$ jeżeli są one równe, tzn. ${\displaystyle aH=Ha,}$ to mówi się wtedy po prostu o warstwach (obustronnych).

Moc zbioru ${\displaystyle G/H=\{aH\colon a\in G\},}$ oznaczanego też ${\displaystyle G:H,}$ wszystkich warstw lewostronnych nazywa się indeksem podgrupy ${\displaystyle H}$ względem grupy ${\displaystyle G}$ i oznacza jednym z symboli ${\displaystyle [G:H],(G:H)}$ lub ${\displaystyle |G:H|}$^[1][2]; tak samo oznacza się i nazywa moc zbioru ${\displaystyle G\backslash H=\{Ha\colon a\in G\}}$ (nie mylić z różnicą zbiorów ${\displaystyle G\smallsetminus H}$) wszystkich warstw prawostronnych, gdyż liczby te są równe (zob. dalej). Spotyka się również odwrócone oznaczenie zbioru warstw prawostronnych, mianowicie ${\displaystyle H\backslash G}$ (bywa ono stosowane jako element notacji warstw podwójnych); jest ono o tyle „bezpieczniejsze”, iż zawsze ${\displaystyle H\smallsetminus G=\varnothing .}$ Jeżeli ${\displaystyle N}$ jest podgrupą normalną, to ${\displaystyle G/N=G\backslash N}$ (zob. Normalność) i wtedy zbiór warstw^[i] oznacza się zwykle wyłącznie za pomocą pierwszego z przytoczonych symboli, tj. jak zbiór warstw lewostronnych^[j].

Własności

Jeżeli ${\displaystyle e}$ oznacza element neutralny w ${\displaystyle G,}$ to warstwa lewostronna ${\displaystyle eH}$ równa jest podgrupie ${\displaystyle H,}$ a ta jest równa warstwie prawostronnej ${\displaystyle He}$^[k] (warstwa ta jest jedyną wśród nich podgrupą, gdyż tylko ona zawiera element neutralny); równości ${\displaystyle aH=H}$ oraz ${\displaystyle Ha=H}$ zachodzą wtedy i tylko wtedy, gdy ${\displaystyle a\in H}$^[l]. Równość ${\displaystyle aH=bH}$ warstw lewostronnych zachodzi wtedy i tylko wtedy, gdy ${\displaystyle a=bh}$ dla pewnego ${\displaystyle h\in H}$^[m], co wprost z definicji warstwy jest równoważne warunkowi ${\displaystyle a\in bH,}$ bądź ${\displaystyle a^{-1}b\in H}$^[n], który można również zastąpić równością ${\displaystyle a^{-1}bH=H}$^[o]; podobnie dla warstw prawostronnych^[p].

Grupa ${\displaystyle G}$ jest sumą parami rozłącznych warstw lewostronnych^[q] i podobnie dla warstw prawostronnych; innymi słowy warstwy lewo- i prawostronne względem ${\displaystyle H}$ wprowadzają odpowiednio podziały ${\displaystyle G/H}$ oraz ${\displaystyle G\backslash H}$ w zbiorze elementów grupy ${\displaystyle G}$ (które nie muszą być identyczne, zob. kolejną sekcję i Przykłady). Ze wzajemnej odpowiedniości podziałów i relacji równoważności wynika, że wspomniane podziały można uzyskać za pomocą relacji równoważności ${\displaystyle \sim }$ bądź ${\displaystyle \backsim }$ utożsamiających elementy z jednej warstwy lewo- bądź prawostronnej, tzn. ${\displaystyle a\sim b\Leftrightarrow aH=bH}$ albo ${\displaystyle a\backsim b\Leftrightarrow Ha=Hb}$ (por. wzór Motywacja); opierając się na powyższych własnościach równości warstw, relacje te definiuje się zwykle za pomocą równoważnych wzorów^[r]

${\displaystyle a\sim b\Leftrightarrow a^{-1}b\in H\quad {\text{ oraz }}\quad a\backsim b\Leftrightarrow ab^{-1}\in H,}$

przy czym klasy równoważności ${\displaystyle [a]_{\sim }}$ mają postać warstw lewostronych ${\displaystyle aH,}$ a klasy równoważności ${\displaystyle [a]_{\backsim }}$ są warstwami prawostronnymi ${\displaystyle Ha}$^[s]. Wynika stąd, że zbiory ilorazowe ${\displaystyle G/\sim }$ oraz ${\displaystyle G/\backsim }$ odpowiadają odpowiednio podziałom ${\displaystyle G/H}$ oraz ${\displaystyle G\backslash H;}$ własności warstw można więc wywnioskować z własności klas równoważności: w szczególności dwie warstwy lewostronne (prawostronne) względem ${\displaystyle H}$ są rozłączne, każdy element grupy ${\displaystyle G}$ należy do jednej i tylko jednej z nich, a ponadto żadna z nich nie jest pusta (zawiera przynajmniej jeden element)^[t].

Sztywność struktury grupy gwarantuje więcej: warstwy lewostronne są równoliczne, podobnie ma się rzecz z warstwami prawostronnymi^[u]. Podgrupa ${\displaystyle H}$ jest równocześnie warstwą lewo- i prawostronną – dlatego równoliczne są wszystkie warstwy (${\displaystyle aH}$ oraz ${\displaystyle Ha}$ dla dowolnego ${\displaystyle a\in G}$) grupy ${\displaystyle G}$ względem ${\displaystyle H;}$ w szczególności jeżeli rząd ${\displaystyle |H|}$ jest skończony, to ${\displaystyle |aH|=|Ha|=|H|}$ dla każdego ${\displaystyle a\in G}$^[v]. Sytuacja ta jest warta podkreślenia, gdyż klasy abstrakcji dowolnych relacji równoważności określonych na zbiorach, np. elementów grupy, nie muszą być równoliczne (zob. rysunek w sekcji Motywacja). Równoliczne są również same podziały ${\displaystyle G/H}$ oraz ${\displaystyle G\backslash H}$ złożone odpowiednio z warstw lewo- i prawostronnych^[w], a ich wspólna moc ${\displaystyle [G:H]}$ nazywana jest indeksem ${\displaystyle H}$ w ${\displaystyle G.}$ Wprost stąd wynika, że na skończony rząd ${\displaystyle G}$ składa się rząd pojedynczej warstwy grupy ${\displaystyle G}$ względem podgrupy ${\displaystyle H}$ pomnożony przez ich liczbę, tzn. zachodzi wzór^[x]

${\displaystyle |G|=|H|\cdot [G:H]}$

(przy oznaczeniach z sekcji Motywacja jest ${\displaystyle |G|=|\ker \varphi |\cdot |\mathrm {im} \ \varphi |}$^[y]). Powyższy wynik, wyrażony zwykle w postaci: rząd podgrupy jest dzielnikiem rzędu grupy, nazywa się zwykle twierdzeniem Lagrange’a, choć niekiedy nazwę tę nosi nieprecyzyjnie bezpośredni z niego wniosek: rząd elementu jest dzielnikiem rzędu grupy^[z] (zob. rząd elementu i grupy).

Normalność

Każda warstwa prawostronna względem podgrupy ${\displaystyle H}$ może być postrzegana jako warstwa lewostronna względem podgrupy ${\displaystyle H^{a}=a^{-1}Ha}$ do niej sprzężonej, gdyż ${\displaystyle aH^{a}=aa^{-1}Ha=Ha}$ dla dowolnego ${\displaystyle a\in G.}$ Z tego powodu mylące może być mówienie o warstwach względem danej podgrupy bez wskazywania, czy chodzi o warstwy lewo-, czy prawostronne. Nie mniej uwaga ta podsuwa pomysł na to jak zapewnić, by relacje ${\displaystyle \sim }$ oraz ${\displaystyle \backsim }$ dawały jeden zbiór ilorazowy ${\displaystyle G/\sim =G/\backsim ,}$ tzn. podgrupa ${\displaystyle H}$ wyznaczała jeden podział ${\displaystyle G/H=G\backslash H}$ w grupie ${\displaystyle G.}$ Mianowicie ${\displaystyle [a]_{\sim }=[a]_{\backsim },}$ czyli ${\displaystyle aH=Ha}$ dla dowolnego ${\displaystyle a\in G;}$ podgrupy ${\displaystyle H}$ grupy ${\displaystyle G}$ spełniające podany warunek nazywa się normalnymi; innymi słowy podgrupy normalne to podgrupy, które (jako całość) są przemienne ze wszystkimi elementami grupy ${\displaystyle G}$^[aa][ab].

Jeżeli podgrupa ${\displaystyle H}$ nie jest normalna, to mimo ich wspólnego indeksu podziały ${\displaystyle G}$ na warstwy lewo- i prawostronne względem ${\displaystyle H}$ są istotnie różne. Mimo to mogą istnieć pojedyncze warstwy ${\displaystyle aH,Ha}$ dla pewnego ${\displaystyle a\in G,}$ które są równe, tzn. ${\displaystyle aH=Ha;}$ sytuacja ta zachodzi np. wtedy, gdy element ${\displaystyle a}$ jest przemienny z dowolnym elementem grupy, tj. należy do centrum ${\displaystyle G}$ (w szczególności jest tak dla ${\displaystyle a=e}$).

Normalność podgrupy ${\displaystyle H}$ jest równoważna temu, by mogła być ona jądrem homomorfizmu grupy ${\displaystyle G,}$ co z kolei umożliwia określenie na zbiorze warstw ${\displaystyle G/H}$ działania ich mnożenia ${\displaystyle \cdot }$ danego wzorem

${\displaystyle (aH)\cdot (bH)=(ab)H.}$

Zbiór ${\displaystyle G/H}$ tworzy wraz z tym działaniem grupę nazywaną grupą ilorazową. W grupach przemiennych, w których korzysta się zwykle z notacji addytywnej, warstwy lewo- i prawostronne grupy ${\displaystyle A}$ względem podgrupy ${\displaystyle B}$ wyznaczane przez element ${\displaystyle a}$ są zawsze równe, ${\displaystyle a+B=B+a}$ (wprost z ich definicji), czyli każda podgrupa jest normalna; stąd grupa ilorazowa ${\displaystyle A/B}$ istnieje dla dowolnej podgrupy ${\displaystyle B}$ grupy przemiennej ${\displaystyle A}$^[j].

Przykłady

Dla dowolnej grupy ${\displaystyle G}$ warstwami (lewo- i prawostronnymi) względem podgrupy trywialnej ${\displaystyle E=\{e\}}$ są wszystkie jej podzbiory jednoelementowe zbioru ${\displaystyle G;}$ z drugiej strony jedyną warstwą (tak lewo- jak i prawostronną) względem jej podgrupy niewłaściwej (tzn. ${\displaystyle G}$) jest cała grupa ${\displaystyle G.}$ W pierwszym przypadku odpowiednia relacja równoważności utożsamia każdy element grupy sam ze sobą, w drugim tożsame są wszystkie elementy grupy^[ac]. Dla obu podgrup podziały wyznaczone są jednoznacznie, co oznacza, że tak

• podgrupa trywialna, jak i niewłaściwa są normalne w dowolnej grupie.

Niech ${\displaystyle G=\mathbb {Z} }$ będzie grupą liczb całkowitych z dodawaniem, a ${\displaystyle H=2\mathbb {Z} }$ będzie zbiorem liczb parzystych. Ponieważ dla dowolnych elementów ${\displaystyle a,b\in H}$ zachodzi ${\displaystyle a-b\in H}$^[ad], to zbiór ${\displaystyle H}$ spełnia kryterium bycia podgrupą w ${\displaystyle G.}$ Istnieją dwie warstwy lewostronne ${\displaystyle G}$ względem ${\displaystyle H,}$ które tworzą odpowiednio zbiory parzystych i nieparzystych liczb całkowitych:

${\displaystyle 0+2\mathbb {Z} =\{2k\colon k\in \mathbb {Z} \}\quad {\text{ oraz }}\quad 1+2\mathbb {Z} =\{1+2k\colon k\in \mathbb {Z} \};}$

istnieją również dokładnie dwie warstwy prawostronne postaci

${\displaystyle 2\mathbb {Z} +0=\{2k\colon k\in \mathbb {Z} \}\quad {\text{ oraz }}\quad 2\mathbb {Z} +1=\{2k+1\colon k\in \mathbb {Z} \},}$

które są równe odpowiadającym im warstwom lewostronnym. Ta sytuacja jest przypadkiem szczególnym następnych dwóch ogólnych reguł mówiących, kiedy warstwy lewostronne są równe prawostronnym (tj. dwóch niezależnych warunków wystarczających na normalność podgrupy):

• istnieje jeden podział na warstwy względem danej podgrupy, o ile tylko działanie w grupie jest przemienne (grupa jest abelowa)^[ae];
• wszystkie podziały dwuelementowe na warstwy względem danej podgrupy są równe (podgrupa jest indeksu 2)^[af].

Wspomniane podziały wyznaczane są przez (tożsame) relacje równoważności

${\displaystyle a\sim b\Leftrightarrow -a+b\in 2\mathbb {Z} \quad {\text{ oraz }}\quad a\backsim b\Leftrightarrow a-b\in 2\mathbb {Z} ,}$

które wyrażają tę samą własność: dwa elementy uważane są za równoważne, jeżeli ich różnica jest liczbą parzystą. Analogicznie rozpatrywać można warstwy ${\displaystyle n\mathbb {Z} }$ dla dowolnej nieujemnej liczby całkowitej ${\displaystyle n;}$ prowadzi to wprost do tzw. arytmetyki modulo ${\displaystyle n}$ (są to grupy ilorazowe przemiennej grupy ${\displaystyle \mathbb {Z} }$ względem ich podgrup ${\displaystyle n\mathbb {Z} }$ dla ${\displaystyle n\in \mathbb {N} }$).

Grupa permutacji ${\displaystyle S_{3}}$ ma tę samą strukturę, co grupa symetrii (tj. grupa izometrii) trójkąta równobocznego (zob. grupa euklidesowa): ${\displaystyle \tau _{i}}$ ${\displaystyle (i=1,2,3)}$ odpowiadają symetriom osiowym (o osiach przechodzących przez dany wierzchołek i środek przeciwległego do niego boku), zaś ${\displaystyle \sigma _{\mathrm {L} }}$ i ${\displaystyle \sigma _{\mathrm {R} }}$ odpowiadają obrotom (o 120°, −120°) wokół środka tego trójkąta; ${\displaystyle \iota }$ odpowiada przekształceniu tożsamościowemu. (Por. grupa diedralna, działanie grupy na zbiorze).

Niech dany będzie trójelementowy zbiór; jego elementy można uporządkować w różnorodny sposób, uzyskując ${\displaystyle 6}$ różnych ciągów. Zmiany uporządkowania możliwe są dzięki tzw. permutacjom, czyli przekształceniom ustalającym porządek elementów danego zbioru; we wspomnianym przypadku wszystkie permutacje zbioru trójelementowego tworzą grupę permutacji ${\displaystyle S_{3}}$ rzędu ${\displaystyle 6}$^[ag] (jest to najmniejsza, w sensie liczby elementów, grupa nieprzemienna). Grupa ta ma cztery nietrywialne podgrupy właściwe^[ah] (wszystkie cykliczne): trzy rzędu ${\displaystyle 2}$ i jedną rzędu ${\displaystyle 3;}$ ostatnia z nich jest normalna, tj. wyznacza podział w ${\displaystyle S_{3}}$ jednoznacznie (gdyż jest on dwuelementowy), każda z trzech pozostałych – nie jest normalna, czyli rozpatrywanie warstw lewo- i prawostonnych wprowadza dwa istotnie różne podziały. Niech przekształcenie ${\displaystyle \iota \colon (1,2,3)\mapsto (1,2,3)}$ oznacza zachowanie uporządkowania (element neutralny), a ${\displaystyle \tau _{3}\colon (1,2,3)\mapsto (2,1,3)}$ oznacza zmianę uporządkowania polegające na przestawieniu dwóch pierwszych elementów (zachowaniu wyłącznie trzeciego elementu) – wspomniane dwie permutacje ${\displaystyle \iota ,\tau _{3}}$ tworzą podgrupę ${\displaystyle H}$ grupy ${\displaystyle G=S_{3}.}$ Warstwami lewo- i prawostronnymi ${\displaystyle G}$ względem ${\displaystyle H}$ są odpowiednio

${\displaystyle \{\iota ,\tau _{3}\},\{\sigma _{\mathrm {L} },\tau _{2}\},\{\sigma _{\mathrm {R} },\tau _{1}\}\quad {\text{ oraz }}\quad \{\iota ,\tau _{3}\},\{\sigma _{\mathrm {R} },\tau _{2}\},\{\sigma _{\mathrm {L} },\tau _{1}\},}$

które są istotnie różne (jedynym wspólnym elementem tych podziałów jest podgrupa ${\displaystyle H}$), gdzie ${\displaystyle \tau _{i}}$ ${\displaystyle (i=1,2,3)}$ to przestawienia dwóch elementów zachowujące ${\displaystyle i}$-ty, zaś ${\displaystyle \sigma _{\mathrm {L} },\sigma _{\mathrm {R} }}$ to cykliczne przestawienia wszystkich elementów odpowiednio „w lewo” i „w prawo”, tzn. ${\displaystyle \sigma _{\mathrm {L} }\colon (1,2,3)\mapsto (3,1,2)}$ oraz ${\displaystyle \sigma _{\mathrm {R} }\colon (1,2,3)\mapsto (2,3,1).}$

Uogólnienia

Niech ${\displaystyle G}$ będzie grupą, a ${\displaystyle H}$ i ${\displaystyle K}$ jej dowolnymi podgrupami. Podzbiory grupy ${\displaystyle G}$ postaci

${\displaystyle HaK=\{hak\colon h\in H,k\in K\}}$

dla ${\displaystyle a\in G}$ nazywa się warstwami podwójnymi grupy ${\displaystyle G}$ względem ${\displaystyle H}$ oraz ${\displaystyle K}$ wyznaczonymi przez element ${\displaystyle a.}$

Zbiór ${\displaystyle H\backslash G/K=\{HaK\colon a\in G\}}$ wszystkich warstw podwójnych grupy ${\displaystyle G}$ względem ${\displaystyle H}$ oraz ${\displaystyle K}$ stanowi rozbicie grupy ${\displaystyle G}$ na rozłączne podzbiory^[ai], jak miało to miejsce w przypadku zwykłych warstw, choć w moc tego zbioru nie musi dzielić rzędu grupy, a same warstwy mogą mieć różne moce, które również nie muszą dzielić rzędu grupy (por. przykłady niżej). Istnieje jednak następujący odpowiednik „wzorów indeksowych” ${\displaystyle |G|=|H||G/H|}$ oraz ${\displaystyle |G|=|H||H\backslash G|}$^[aj]:

Twierdzenie Frobeniusa

Niech ${\displaystyle G}$ będzie grupą skończoną, a ${\displaystyle H,K}$ jej podgrupami. Wówczas

${\displaystyle {\Big |}{\big \{}(h,g,k)\in H\times G\times K\colon hgk=g{\big \}}{\Big |}=|H|\,|K|\,{\big |}H\backslash G/K{\big |}.}$

Przykłady

Zwykłe warstwy są przypadkiem szczególnym warstw podwójnych, w których jedna z podgrup jest trywialna: ${\displaystyle HaE=Ha}$ oraz ${\displaystyle EaK=aK,}$ gdzie ${\displaystyle E=\{e\}}$ zawiera wyłącznie element neutralny ${\displaystyle e}$ grupy ${\displaystyle G.}$ Podobnie ${\displaystyle H\backslash G/K}$ staje się zbiorem warstw lewo- bądź prawostronnych. Jak odwracanie przekształcało ${\displaystyle G/H}$ na ${\displaystyle H\backslash G}$ (bijekcja ustalająca równoliczność warstw lewo- i prawostronnych), tak przekształca ono ${\displaystyle H\backslash G/K}$ na ${\displaystyle K\backslash G/H.}$

Jeżeli ${\displaystyle G}$ jest przemienna, to iloczyn (kompleksowy) zbiorów ${\displaystyle HK}$ tworzy podgrupę w ${\displaystyle G,}$ a warstwy podwójne względem ${\displaystyle H}$ oraz ${\displaystyle K}$ są po prostu zwykłymi warstwami względem podgrupy ${\displaystyle HK.}$

Niech dana będzie grupa ${\displaystyle G=S_{3}}$ z oznaczeniami z sekcji Przykłady. Jeżeli ${\displaystyle H=\{\iota ,\tau _{3}\},}$ zaś ${\displaystyle K=\{\iota ,\tau _{2}\},}$ to warstwą podwójną względem tych podgrup wyznaczoną przez ${\displaystyle \iota }$ jest

${\displaystyle H\iota K=HK=\{hk\colon h\in H,k\in K\}=\{\iota ,\tau _{2},\tau _{3},\sigma _{\mathrm {L} }\},}$

z kolei ${\displaystyle \tau _{1}}$ wyznacza warstwę

${\displaystyle H\tau _{1}K=\{\iota \tau _{1}\iota ,\ \iota \tau _{1}\tau _{2},\ \tau _{3}\tau _{1}\iota ,\ \tau _{3}\tau _{1}\tau _{2}\}=\{\tau _{1},\sigma _{\mathrm {R} }\}.}$

Są to wszystkie warstwy wyznaczane przez te dwie podgrupy. Jeśli ${\displaystyle H=K=\{\iota ,\tau _{3}\},}$ to istnieją tylko dwie warstwy podwójne: ${\displaystyle H\iota H=HH=H=\{\iota ,\tau _{3}\}}$ oraz ${\displaystyle H\tau _{2}H=\{\tau _{2},\tau _{1},\sigma _{\mathrm {L} },\sigma _{\mathrm {R} }\}.}$

Niech ${\displaystyle G=D_{4}=\langle \mathrm {r} ,\mathrm {s} \rangle }$ będzie grupą diedralną oraz ${\displaystyle H=K=\{\mathrm {id} ,\mathrm {s} \},}$ gdzie ${\displaystyle \mathrm {r} ,\mathrm {s} }$ oznaczają odpowiednio elementy rzędu 4 i 2 (obrót i symetrię). Różnymi warstwami dwustronnymi względem ${\displaystyle H}$ (oraz ${\displaystyle H}$) są:

${\displaystyle HH=H=\left\{\mathrm {id} ,\mathrm {s} \right\},\quad H\mathrm {r} H=\left\{\mathrm {r} ,\mathrm {rs} ,\mathrm {r} ^{3}\mathrm {s} ,\mathrm {r} ^{3}\right\},\quad H\mathrm {r} ^{2}H=\left\{\mathrm {r} ^{2},\mathrm {r} ^{2}\mathrm {s} \right\}.}$

Zobacz też

• iloczyn kompleksowy
• kongruencja

Uwagi

Przypisy

Bibliografia

• Andrzej Białynicki-Birula: Algebra. Warszawa: Wydawnictwo Naukowe PWN, 2009, s. 232. ISBN 978-83-01-15817-0.
• Bolesław Gleichgewicht: Algebra. Wrocław: Oficyna Wydawnicza GiS, 2004, s. 265–266. ISBN 978-83-89020-35-2.

Literatura dodatkowa

• Jerzy Browkin: Teoria ciał. T. 49. Warszawa: Państwowe Wydawnictwo Naukowe, 1978, seria: Biblioteka Matematyczna.
• William Raymond Scott: Group theory. Nowy Jork: Dover Publications Inc., 2012, s. 20–21, 30–31. ISBN 978-0-486-65377-8.