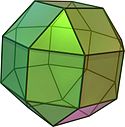
Wielościan półforemny
Wielościan półforemny (albo archimedesowy[1] – od imienia Archimedesa z Syrakuz) – wielościan, którego ściany są wielokątami foremnymi, w każdym wierzchołku zbiega się jednakowa liczba ścian, jednak poszczególne ściany różnią się od siebie oraz istnieje izometria przekształcająca każdy wierzchołek na każdy inny (warunek wierzchołkowej tranzytywności)[2][a].
Jeśli ściany są przystającymi wielokątami foremnymi, wielościan nazwany jest foremnym (platońskim).
Istnieje 13 wielościanów półforemnych (15 jeśli liczyć odbicia lustrzane dwóch spośród nich) oraz dwie nieskończone serie.
Nieskończone serie
- graniastosłupy archimedesowe
- antygraniastosłupy
Pozostałe wielościany półforemne
| Nazwa (Konfiguracja wektorowa) | Grafika przejrzysta | Grafika nieprzejrzysta | Siatka | Ściany | Krawędzie | Wierzchołki | Grupa symetryczna | |
|---|---|---|---|---|---|---|---|---|
| Czworościan ścięty (3.6.6) |  (Animacja) |  | 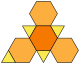 | 8 | 4 trójkąty 4 sześciokąty | 18 | 12 | Td |
| Sześcio-ośmiościan (3.4.3.4) |  (Animacja) |  | 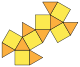 | 14 | 8 trójkątów 6 kwadratów | 24 | 12 | Oh |
| Sześcian ścięty (3.8.8) |  (Animacja) |  | 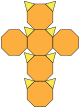 | 14 | 8 trójkątów 6 ośmiokątów | 36 | 24 | Oh |
| Ośmiościan ścięty (4.6.6) |  (Animacja) |  |  | 14 | 6 kwadratów 8 sześciokątów | 36 | 24 | Oh |
| Sześcio-ośmiościan rombowy mały (3.4.4.4) |  (Animacja) |  | 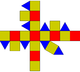 | 26 | 8 trójkątów 18 kwadratów | 48 | 24 | Oh |
| Sześcio-ośmiościan rombowy wielki (4.6.8) |  (Animacja) |  | 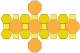 | 26 | 12 kwadratów 8 sześciokątów 6 ośmiokątów | 72 | 48 | Oh |
| Sześcio-ośmiościan przycięty (3.3.3.3.4) |  (Animacja)  (Animacja) |  |  | 38 | 32 trójkąty 6 kwadratów | 60 | 24 | O |
| Dwudziesto-dwunastościan (3.5.3.5) | 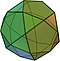 (Animacja) |   |  | 32 | 20 trójkątów 12 pięciokątów | 60 | 30 | Ih |
| Dwunastościan ścięty (3.10.10) | 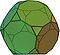 (Animacja) |  |  | 32 | 20 trójkątów 12 dziesięciokątów | 90 | 60 | Ih |
| Dwudziestościan ścięty (5.6.6) |  (Animacja) |  |  | 32 | 12 pięciokątów 20 sześciokątów | 90 | 60 | Ih |
| Dwudziesto-dwunastościan rombowy mały (3.4.5.4) |  (Animacja) |  |  | 62 | 20 trójkątów 30 kwadratów 12 pięciokątów | 120 | 60 | Ih |
| Dwudziesto-dwunastościan rombowy wielki (4.6.10) |  (Animacja) |  |  | 62 | 30 kwadratów 20 sześciokątów 12 dziesięciokątów | 180 | 120 | Ih |
| Dwudziesto-dwunastościan przycięty (3.3.3.3.5) |  (Animacja)  (Animacja) |  |  | 92 | 80 trójkątów 12 pięciokątów | 150 | 60 | I |
Uwagi
Przypisy
- ↑ wielościan archimedesowy, [w:] Encyklopedia PWN [online] [dostęp 2021-10-02].
- ↑ a b Pseudo sześcio-ośmiościany rombowe. matematyka.wroc.pl, 2008-09-05. [dostęp 2015-06-25].
Media użyte na tej stronie
Snub dodecahedron ccw.png
Left-handed (anti-clockwise) snub dodecahedron. The yellow triangles define the "handedness" of the object. In this case, if we start with the rhombicosidodecahedron shown here and rotate the pentagons anti-clockwise allowing the yellow squares to deform into two equilateral triangles, we end up with the shape shown above.
Left-handed (anti-clockwise) snub dodecahedron. The yellow triangles define the "handedness" of the object. In this case, if we start with the rhombicosidodecahedron shown here and rotate the pentagons anti-clockwise allowing the yellow squares to deform into two equilateral triangles, we end up with the shape shown above.
Icosidodecaëder.png
ruimtelijk figuur - eigen werk ism danielm - publiek domein
ruimtelijk figuur - eigen werk ism danielm - publiek domein
Truncated tetrahedron flat.svg
Autor: Júlio Reis, Licencja: CC BY-SA 3.0
A flattened truncated tetrahedron.
Autor: Júlio Reis, Licencja: CC BY-SA 3.0
A flattened truncated tetrahedron.
Truncated cuboctahedron flat.svg
Autor: Júlio Reis, Licencja: CC BY-SA 3.0
Flattened net of a truncated cuboctahedron.
Autor: Júlio Reis, Licencja: CC BY-SA 3.0
Flattened net of a truncated cuboctahedron.
Truncated hexahedron flat.svg
Autor: Júlio Reis, Licencja: CC BY-SA 3.0
Flattened truncated hexahedron. SVG version.
Autor: Júlio Reis, Licencja: CC BY-SA 3.0
Flattened truncated hexahedron. SVG version.
Cuboctahedron.png
Image d'un cuboctaèdre
Image d'un cuboctaèdre
Cuboctahedron.svg
Autor: w:en:User:Cyp, Licencja: CC-BY-SA-3.0
Ta ^specifik^ z W3C grafika wektorowa została stworzona za pomocą Inkscape .
Autor: w:en:User:Cyp, Licencja: CC-BY-SA-3.0
Ta ^specifik^ z W3C grafika wektorowa została stworzona za pomocą Inkscape .