Wielościany Catalana

Wielościany Catalana (bryły Catalana) – wielościany dualne do wielościanów archimedesowych^[1]. Wielościan dualny powstaje przez zastąpienie każdej ściany wierzchołkiem, a każdego wierzchołka ścianą.

Wszystkie wielościany są wypukłe. Ich grupy symetrii są przechodnie ze względu na ściany, ale nieprzechodnie ze względu na wierzchołki. Jest tak, ponieważ dualne do nich wielościany archimedesowe mają grupy symetrii przechodnie ze względu na wierzchołki i nieprzechodnie ze względu na ściany. W przeciwieństwie do brył platońskich i brył archimedesowych, ściany brył Catalana nie są wielokątami foremnymi. Ponadto dwie z brył Catalana mają grupy symetrii przechodnie ze względu na krawędzie: dwunastościan rombowy i trzydziestościan rombowy.

Dwa z wielościanów Catalana są chiralne: dwudziestoczterościan pięciokątny i sześćdziesięciościan pięciokątny, dualne do chiralnych brył Archimedesa: sześcio-ośmiościanu przyciętego i dwudziesto-dwunastościanu przyciętego.

Nazwa pochodzi od nazwiska belgijskiego matematyka Eugèna Charlesa Catalana.

Nazwa(s)	Rysunek obrotowy bryły	Siatka	Wielościan dualny (bryła Archimedesa)	Ściany	Krawędzie	Wierzchołki	Konfiguracja ścian	Symetria
czworościan potrójny	(animacja)		czworościan ścięty	12	18	8	trójkąt równoramienny V3.6.6	${\displaystyle T_{d}}$
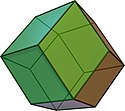
dwunastościan rombowy	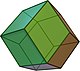(animacja)		sześcio-ośmiościan	12	24	14	Romb V3.4.3.4	${\displaystyle O_{h}}$
ośmiościan potrójny	(c) Cyp, CC-BY-SA-3.0 (animacja)		sześcian ścięty	24	36	14	trójkąt równoramienny V3.8.8	${\displaystyle O_{h}}$
sześcian poczwórny	(animacja)		ośmiościan ścięty	24	36	14	trójkąt równoramienny V4.6.6	${\displaystyle O_{h}}$
dwudziestoczterościan deltoidowy	(animacja)		sześcio-ośmiościan rombowy mały	24	48	26	Deltoid V3.4.4.4	${\displaystyle O_{h}}$
ośmiościan szóstkowy	(animacja)		sześcio-ośmiościan ścięty	48	72	26	trójkąt różnoboczny V4.6.8	${\displaystyle O_{h}}$
dwudziestoczterościan pięciokątny	(anim.)(anim.)		sześcio-ośmiościan przycięty	24	60	38	pięciokąt nieforemny V3.3.3.3.4	${\displaystyle O}$
trzydziestościan rombowy	(animacja)		dwudziesto-dwunastościan	30	60	32	Romb V3.5.3.5	${\displaystyle I_{h}}$
dwudziestościan potrójny	(animacja)		dwunastościan ścięty	60	90	32	trójkąt równoramienny V3.10.10	${\displaystyle I_{h}}$
dwunastościan piątkowy	(animacja)		dwudziestościan ścięty	60	90	32	trójkąt równoramienny V5.6.6	${\displaystyle I_{h}}$
sześćdziesięciościan deltoidalny	(animacja)		dwudziesto-dwunastościan rombowy mały	60	120	62	deltoid V3.4.5.4	${\displaystyle I_{h}}$
dwudziestościan szóstkowy	(animacja)		dwudziesto-dwunastościan ścięty	120	180	62	trójkąt różnoboczny V4.6.10	${\displaystyle I_{h}}$
sześćdziesięciościan pięciokątny	(anim.)(anim.)		dwudziesto-dwunastościan przycięty	60	150	92	pięciokąt nieforemny V3.3.3.3.5	${\displaystyle I}$

Przypisy