Wzór Eulera

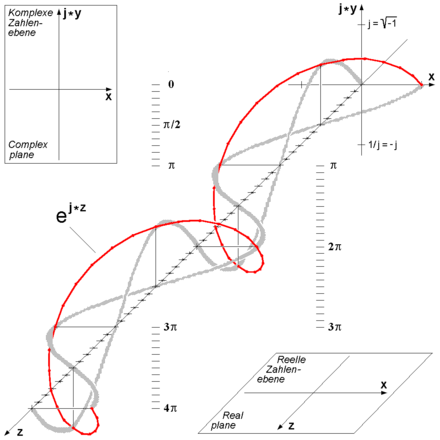
Trójwymiarowa ilustracja wzoru Eulera

Wzór Eulera – wzór analizy zespolonej wiążący funkcje trygonometryczne z zespoloną funkcją wykładniczą, określany nazwiskiem Leonharda Eulera.

Wzór

Niech ${\displaystyle x\in \mathbb {R} ,}$ zaś ${\displaystyle i}$ jest jednostką urojoną, wtedy wzór Eulera ma postać^[1]:

${\displaystyle e^{ix}=\cos x+i\sin x}$.

Historia

Wzór Eulera został dowiedziony po raz pierwszy przez Rogera Cotesa w 1714 w postaci

${\displaystyle \ln(\cos x+i\sin x)=ix.}$

Euler jako pierwszy opublikował go w formie „standardowej” – tej, która później stała się najczętszą. Zrobił to w 1748, opierając swój dowód na równości szeregów po obu stronach tożsamości. Żaden z nich nie podał interpretacji geometrycznej tego wzoru: utożsamienie liczb zespolonych z płaszczyzną zespoloną powstało około 50 lat później (wynik Caspara Wessela).

Dowód

Rozwinięte w szereg potęgowy funkcje ${\displaystyle e^{x},\sin x,\cos x}$ przyjmują postać^[2]:

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\dots =\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}},}$

${\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\dots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},}$

${\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\dots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.}$

Powyższe wzory służą jako definicje zespolonych funkcji exp, sin i cos, tzn. definiuje się funkcje:

${\displaystyle \exp :\mathbb {C} \to \mathbb {C} ,\ \exp z:=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}}$^[3],

${\displaystyle \sin :\ \mathbb {C} \to \mathbb {C} ,\ \sin z:=\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{(2n+1)!}}}$^[4],

${\displaystyle \cos :\mathbb {C} \to \mathbb {C} ,\ \cos z:=\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n}}{(2n)!}}}$^[4].

Definicje te są poprawne, ponieważ szeregi występujące po prawej stronie są zbieżne dla każdego ${\displaystyle z\in \mathbb {C} ,}$ gdyż kryteria zbieżności szeregów takie jak kryterium d’Alemberta i kryterium Cauchy’ego pozostają prawdziwe dla liczb zespolonych^[5].

W szczególności mamy: ${\displaystyle e^{iz}=1+iz+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+\dots =\left(1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-\dots \right)+i\left(z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-\dots \right)=\cos z+i\sin z,}$

gdzie skorzystaliśmy z tego, że:

• jeżeli szeregi ${\displaystyle \sum _{n}a_{n}}$ oraz ${\displaystyle \sum _{n}b_{n}}$ są zbieżne, to zbieżny jest również szereg ${\displaystyle \sum _{n}(a_{n}+b_{n}),}$ oraz: ${\displaystyle \sum _{n=0}^{\infty }(a_{n}+b_{n})=\sum _{n=0}^{\infty }a_{n}+\sum _{n=0}^{\infty }b_{n},}$ (addytywność);
• jeżeli szereg ${\displaystyle \sum _{n}a_{n}}$ jest zbieżny, to również szereg ${\displaystyle \sum _{n}ca_{n}}$ jest zbieżny, oraz ${\displaystyle \sum _{n=0}^{\infty }ca_{n}=c\sum _{n=0}^{\infty }a_{n},}$ gdzie c jest stałą (jednorodność).

Powrót do liczb rzeczywistych za pomocą podstawienia ${\displaystyle z\mapsto x\in \mathbb {R} }$ daje oryginalną tożsamość opisaną przez Eulera.

Inne uzasadnienie formuły

Niech ${\displaystyle f\colon \mathbb {R} \to \mathbb {C} }$ będzie dana przez ${\displaystyle f(x)=\cos(x)+i\sin(x).}$ Wówczas

${\displaystyle f'(x)=i\cos(x)-\sin(x)=i(\cos(x)+i\sin(x))=if(x).}$

Następnie niech ${\displaystyle g(x)=e^{-ix}f(x).}$ Wtedy

${\displaystyle g'(x)=e^{-ix}(f'(x)-if(x))=0.}$

dla każdego ${\displaystyle x,}$ a stąd ${\displaystyle g}$ jest funkcją stałą. Ponieważ

${\displaystyle g(0)=e^{-i\cdot 0}f(0)=\cos(0)+i\sin(0)=1,}$

mamy ${\displaystyle g(x)=1}$ dla wszystkich ${\displaystyle x.}$ Stąd też ${\displaystyle f(x)=g(x)e^{ix}=e^{ix},}$ czyli

${\displaystyle e^{ix}=\cos(x)+i\sin(x).}$

Przy okazji warto zauważyć, że jest to postać trygonometryczna liczby zespolonej o module jednostkowym.

Trygonometria

Wzór Eulera stanowi powiązanie analizy i trygonometrii, dostarczając interpretację funkcji sinus i cosinus jako sum ważonych funkcji wykładniczej. Odpowiednie wzory można wyprowadzić, budując odpowiedni układ równań:

${\displaystyle {\begin{cases}e^{ix}=\cos x+i\sin x\\e^{-ix}=\cos(-x)+i\sin(-x)\end{cases}}.}$

Korzystając z własności parzystości i nieparzystości funkcji trygonometrycznych:

${\displaystyle {\begin{cases}e^{ix}=\cos x+i\sin x\\e^{-ix}=\cos x-i\sin x\end{cases}}.}$

Po dodaniu stronami:

${\displaystyle e^{ix}+e^{-ix}=2\cos x,}$

${\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}.}$

Analogicznie otrzymuje się wzór:

${\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}.}$

Wzory te mogą służyć jako definicje funkcji trygonometrycznych dla argumentów zespolonych. Przykładowo podstawienie ${\displaystyle x=iy}$ daje:

${\displaystyle \cos(iy)={\frac {e^{-y}+e^{y}}{2}}=\cosh y,}$

${\displaystyle \sin(iy)={\frac {e^{-y}-e^{y}}{2i}}=i\sinh y.}$

Zastosowanie

Tożsamość może zostać wykorzystana jako metoda do upraszczania wyrażeń trygonometrycznych. Wymaga ona co prawda przejścia w rachunkach przez liczby zespolone, ale nie wymaga żadnej wiedzy na ich temat oprócz pamiętania, że ${\displaystyle i^{2}=-1}$ i znajomości poniższych trzech wzorów (funkcje tangens i cotangens określa się tak samo jak w przypadku rzeczywistym):

${\displaystyle \sin x={\tfrac {e^{ix}-e^{-ix}}{2i}},}$

${\displaystyle \cos x={\tfrac {e^{ix}+e^{-ix}}{2}},}$

${\displaystyle e^{ix}=\cos x+i\sin x.}$

Najpierw należy przekształcić upraszczany wzór za pomocą dwóch pierwszych wzorów na postać wykładniczą (w przypadku tangensa i cotangensa, rozbijając go na iloraz funkcji sinus i cosinus), następnie wykonać odpowiednie działania tak, jak na zwykłych potęgach liczb rzeczywistych, a na koniec stosując jeden z wzorów Eulera, wrócić do postaci trygonometrycznej wyrażenia.

Przykłady

Sinus kąta zwielokrotnionego

Dla całkowitych dodatnich ${\displaystyle n}$ wyrażenia postaci ${\displaystyle \sin nx}$ dają się wyrazić za pomocą samych wartości ${\displaystyle \sin x}$ i ${\displaystyle \cos x}$ oraz elementarnych działań.

Korzystając z powyższych wzorów:

${\displaystyle \sin nx={\frac {e^{inx}-e^{-inx}}{2i}}={\frac {(e^{ix})^{n}-(e^{-ix})^{n}}{2i}}.}$

Ze wzoru Eulera:

${\displaystyle \sin nx={\frac {(\cos {x}+i\sin {x})^{n}-(\cos {x}-i\sin {x})^{n}}{2i}}.}$

Z dwumianu Newtona:

${\displaystyle \sin nx=\sum \limits _{k=0}^{n}{n \choose k}{\frac {(\cos {x})^{k}(i\sin {x})^{n-k}-(\cos {x})^{k}(-i\sin {x})^{n-k}}{2i}}.}$

Wyłączając wspólny czynnik:

${\displaystyle \sin nx=\sum \limits _{k=0}^{n}{n \choose k}(\cos {x})^{k}(\sin {x})^{n-k}{\frac {i^{n-k}-(-i)^{n-k}}{2i}}}$

i stosując wzór Eulera, dostajemy ostatecznie

${\displaystyle \sin nx=\sum \limits _{k=0}^{n}{n \choose k}(\cos {x})^{k}(\sin {x})^{n-k}\sin {\frac {(n-k)\pi }{2}}}$

Kilka pierwszych wielokrotności:

${\displaystyle \sin 2x=2\cos x\sin x,}$

${\displaystyle \sin 3x=3\cos ^{2}x\sin x-\sin ^{3}x,}$

${\displaystyle \sin 4x=4\cos ^{3}x\sin x-4\cos x\sin ^{3}x,}$

${\displaystyle \sin 5x=5\cos ^{4}x\sin x-10\cos ^{2}x\sin ^{3}x+\sin ^{5}x.}$

Upraszczanie wyrażeń trygonometrycznych

Sprowadzić do prostszej postaci wyrażenie:

${\displaystyle f(x)=8\cos ^{3}x\sin x-4\cos x\sin x.}$

Korzystając ze wzorów Eulera na sinus i cosinus:

${\displaystyle f(x)=8\left({\frac {e^{ix}+e^{-ix}}{2}}\right)^{3}{\frac {e^{ix}-e^{-ix}}{2i}}-4{\frac {e^{ix}+e^{-ix}}{2}}\cdot {\frac {e^{ix}-e^{-ix}}{2i}}.}$

Po wymnożeniu jest:

${\displaystyle f(x)=(e^{3ix}+3e^{2ix}e^{-ix}+3e^{ix}e^{-2ix}+e^{-3ix}){\frac {e^{ix}-e^{-ix}}{2i}}-{\frac {2e^{2ix}-2e^{-2ix}}{2i}}}$

i dalej:

${\displaystyle f(x)={\frac {e^{4ix}+3e^{2ix}+3+e^{-2ix}-e^{2ix}-3-3e^{-2ix}-e^{-4ix}}{2i}}-{\frac {2e^{2ix}-2e^{-2ix}}{2i}},}$

po skróceniu:

${\displaystyle f(x)={\frac {e^{4ix}-e^{-4ix}}{2i}},}$

dlatego po zastosowaniu pierwszego z podanych wzorów Eulera wyrażenie ma postać:

${\displaystyle f(x)=\sin 4x.}$

Całkowanie funkcji trygonometrycznych przy pomocy wzoru Eulera

Obliczyć całkę:

${\displaystyle \int \sin ^{2}x\cos 4x\,dx.}$

Podstawiając odpowiednie wzory Eulera na sinus i cosinus oraz wymnażając:

${\displaystyle {\begin{aligned}\int \sin ^{2}x\cos 4x\,dx\,&=\,\int \left({\frac {e^{ix}-e^{-ix}}{2i}}\right)^{2}\left({\frac {e^{4ix}+e^{-4ix}}{2}}\right)dx\\[6pt]&=\,-{\frac {1}{8}}\int \left(e^{2ix}-2+e^{-2ix}\right)\left(e^{4ix}+e^{-4ix}\right)dx\\[6pt]&=\,-{\frac {1}{8}}\int \left(e^{6ix}-2e^{4ix}+e^{2ix}+e^{-2ix}-2e^{-4ix}+e^{-6ix}\right)dx.\\&=\,-{\frac {1}{8}}\int \left(\left(e^{6ix}+e^{-6ix}\right)-2\left(e^{4ix}+e^{-4ix}\right)+\left(e^{2ix}+e^{-2ix}\right)\right)dx.\\&=\,-{\frac {1}{8}}\int \left(2\cos 6x-2\cdot 2\cos 4x+2\cos 2x\right)dx.\end{aligned}}}$

W tym miejscu wyrażenie można było scałkować, a dopiero potem zwinąć je do wzorów na sinus i cosinus. Obie metody dają to samo rozwiązanie:

${\displaystyle \int \sin ^{2}x\cos 4x\,dx=-{\frac {1}{24}}\sin 6x+{\frac {1}{8}}\sin 4x-{\frac {1}{8}}\sin 2x+C.}$

Całkowanie funkcji przy pomocy wzoru Eulera i wykorzystanie części rzeczywistej liczby zespolonej

Użycie wzoru Eulera pozwala na całkowanie również innych funkcji, w których pojawiają się wzory trygonometryczne, jak na przykład:

${\displaystyle \int e^{x}\cos x\,dx.}$

ponieważ ${\displaystyle \cos x}$ jest częścią rzeczywistą ${\displaystyle e^{ix}}$ możemy zapisać

${\displaystyle \int e^{x}\cos x\,dx=\operatorname {Re} \int e^{x}e^{ix}\,dx.}$

Całka po prawej stronie jest łatwa do wyliczenia:

${\displaystyle \int e^{x}e^{ix}\,dx=\int e^{(1+i)x}\,dx={\frac {e^{(1+i)x}}{1+i}}+C.}$

A zatem:

${\displaystyle {\begin{aligned}\int e^{x}\cos x\,dx\,&=\,\operatorname {Re} \left\{{\frac {e^{(1+i)x}}{1+i}}\right\}+C\\[6pt]&=\,e^{x}\operatorname {Re} \left\{{\frac {e^{ix}}{1+i}}\right\}+C\\[6pt]&=\,e^{x}\operatorname {Re} \left\{{\frac {e^{ix}(1-i)}{2}}\right\}+C\\[6pt]&=\,e^{x}\,{\frac {\cos x+\sin x}{2}}+C.\end{aligned}}}$

Metody te pomagają przy wyznaczaniu kolejnych współczynników szeregów Fouriera^[6], w których występują całki postaci ${\displaystyle \int _{-a}^{a}f(x)\sin nxdx}$ i ${\displaystyle \int _{-a}^{a}f(x)\cos nxdx.}$

Tożsamość Eulera

Funkcja wykładnicza e^z może być zdefiniowana jako granica ciągu (1+z/N)^N, przy N dążącym do nieskończoności. Powyżej kładziemy z=iπ i rozważamy wartości N od 1 do 100. Obliczanie wartości (1+iπ / N)^N jest przedstawione jako N-krotne powtórzenie mnożenia na płaszczyźnie zespolonej (gdzie ostatni punkt to wartość (1+iπ / N)^N). Zauważmy, że ze zwiększaniem liczby N, liczba zespolona (1+iπ / N)^N zbliża się do −1. Zatem e^iπ=-1.

W szczególności, podstawiając ${\displaystyle x=\pi ,}$ otrzymuje się równość:

${\displaystyle e^{\pi i}+1=0,}$

nazywaną też tożsamością Eulera (czasami wzorem Eulera).

Nie istnieją żadne znane dokumenty potwierdzające autorstwo Eulera; co więcej, była ona zapewne znana matematykom żyjącym przed nim.

„Najpiękniejszy wzór”

Tożsamość Eulera nazywana jest często najpiękniejszym wzorem matematycznym. Wykorzystane są w niej trzy działania arytmetyczne: dodawanie, mnożenie i potęgowanie. Tożsamość łączy pięć fundamentalnych stałych matematycznych:

• liczbę 0,
• liczbę 1,
• liczbę π,
• liczbę e,
• liczbę i, jednostkę urojoną liczb zespolonych.

Dodatkowo każde z powyższych działań oraz każda ze stałych użyte są dokładnie raz, co więcej: wzór ten jest przedstawiony w zwyczajowej formie równania, którego prawa strona jest zerem.

Uogólnienie

Tożsamość Eulera jest przypadkiem szczególnym ogólniejszej tożsamości, w której pierwiastki z jedynki ${\displaystyle n}$-tego stopnia sumują się do ${\displaystyle 0}$ dla ${\displaystyle n>1{:}}$

${\displaystyle \sum _{k=0}^{n-1}e^{\frac {2\pi ik}{n}}=0.}$

Tożsamość Eulera otrzymuje się przez podstawienie ${\displaystyle n=2.}$ Powyższą równość można zapisać i w postaci:

${\displaystyle \sum _{k=0}^{n}e^{\frac {2\pi ik}{n}}=1.}$

ponieważ: ${\displaystyle \exp(2\pi i)=1.}$

Zobacz też

• funkcja wykładnicza
• liczby zespolone
• logarytm naturalny
• stała Gelfonda

Przypisy

Bibliografia

• LechL. Górniewicz LechL., Roman StanisławR.S. Ingarden Roman StanisławR.S., Analiza matematyczna dla fizyków, Toruń: Wydawnictwo Naukowe UMK, 2012 .
• G.I. Zaporożec: Metody rozwiązywania zadań z analizy matematycznej. Warszawa: Wydawnictwa Naukowo-Techniczne, 1973.

Linki zewnętrzne

• Grant Sanderson, Euler’s formula with introductory group theory, kanał 3blue1brown, YouTube, 3 marca 2017 [dostęp 2021-03-15].