Metody wyznaczania rzędu reakcji chemicznej

Metody wyznaczania rzędu reakcji – metody określania stopnia ${\displaystyle (n)}$ wielomianu, jakim jest równanie kinetyczne reakcji, czyli zależność jej szybkości od stężenia reagentów. Doświadczalną podstawą określania wartości ${\displaystyle n}$ są wyniki analiz stężenia reagentów, wykonywanych w czasie biegu reakcji. Zgromadzony zbiór wyników analiz chemicznych poddaje się analizie statystycznej, prowadzonej w celu znalezienia takiego wielomianu:

szybkość ubytku substratu = f (stężenia reagentów),

np. ${\displaystyle -{\frac {dc_{A}}{dt}}=kc_{A}^{n_{A}}c_{B}^{n_{B}}c_{C}^{n_{C}},}$

który najlepiej opisuje wyniki eksperymentu. Stopień tego wielomianu ${\displaystyle (n=n_{A}+n_{B}+n_{C})}$ nazywa się rzędem reakcji, a wykładniki potęg przy stężeniach poszczególnych związków ${\displaystyle (n_{A},\ n_{B},\ n_{C})}$ – rzędem względem tych związków. Symbolem ${\displaystyle k}$ oznacza się stałą szybkości reakcji^[1][2].

W przypadku reakcji elementarnych rząd reakcji ma wartości ${\displaystyle n}$ = 0, 1 lub 2 (reakcja zerowego rzędu, pierwszorzędowa lub drugorzędowa). Inne wartości ${\displaystyle n}$ – większe od 2 lub ułamkowe – świadczą zwykle o tym, że badana reakcja jest złożona^[a]. Wyjaśnienie mechanizmu takich reakcji wymaga stosowania specyficznych metod badawczych, w tym określenia rzędu poszczególnych reakcji elementarnych.

Wśród klasycznych metod wyznaczania rzędu reakcji są wymieniane metody^[1][2]:

• podstawienia do wzoru,
• graficzna,
• różnicowa van ’t Hoffa (1884),
• całkowa Ostwalda i Zawidzkiego,
• izolacyjna Ostwalda.

Metoda podstawienia do wzoru

Wyniki oznaczeń stężenia reagentów ${\displaystyle (c),}$ rejestrowane w czasie ${\displaystyle (t)}$ biegu reakcji, są podstawiane do różnych równań kinetycznych, np. ^[1][2]:

• dla reakcji zerowego rzędu:

${\displaystyle -{\frac {dc_{A}}{dt}}=k}$

• dla reakcji pierwszego rzędu:

${\displaystyle -{\frac {dc_{A}}{dt}}=kc_{A}}$

${\displaystyle \ln {c_{A}}=-kt+\ln {a}}$

• dla reakcji drugiego rzędu

${\displaystyle -{\frac {dc_{A}}{dt}}=kc_{A}^{2}}$

${\displaystyle -{\frac {dc_{A}}{dt}}=-{\frac {dc_{B}}{dt}}=kc_{A}c_{B}.}$

Oblicza się wartości ${\displaystyle k}$ i sprawdza, które z równań prowadzi do wyników niezmiennych (zmienność w granicach błędu pomiarów), czyli do rzeczywistej wartości stałej szybkości reakcji ${\displaystyle (k=\operatorname {const} ).}$

Sprawdzając np. czy dla reakcji A + B wykładnik ${\displaystyle n=2,}$ oblicza się wartości ${\displaystyle k}$ z zależności:

${\displaystyle k={\frac {2{,}303}{a-b}}\cdot \log {\frac {b(a-x)}{a(b-x)}},}$

gdzie: ${\displaystyle a}$ i ${\displaystyle b}$ – początkowe stężenia reagentów, ${\displaystyle (a-x)}$ i ${\displaystyle (b-x)}$ – stężenia chwilowe.

Potwierdzeniem założenia jest uzyskanie wartości ${\displaystyle k,}$ które nie zależą od ${\displaystyle t}$ i ${\displaystyle x.}$

Metoda graficzna

Istota metody, tradycyjnie nazywanej graficzną, nie różni się od „metody podstawienia do wzoru”. W obu przypadkach sprawdza się, które z równań kinetycznych najlepiej odpowiada danym doświadczalnym. W przeszłości wyniki wykonywanych analiz, np. kolejnych oznaczeń stężenia substratu ${\displaystyle c_{A},}$ ręcznie nanoszono na wykresy, sporządzane w tak dobranym układzie współrzędnych, aby wykazanie zależności prostoliniowej świadczyło o określonym rzędzie reakcji^[b]. Linie proste uzyskuje się w układzie współrzędnych^[1][2]:

• ${\displaystyle x=t,\ y=c}$ – gdy reakcja jest zerowego rzędu,
• ${\displaystyle x=t,\ y=\ln c}$ – gdy reakcja jest pierwszego rzędu,
• ${\displaystyle x=t,\ y=1/c}$ – gdy reakcja jest drugiego rzędu,
• ${\displaystyle x=t,\ y=1/c^{2}}$ – gdy reakcja jest trzeciego rzędu.

Jeżeli w każdym z wymienionych układów współrzędnych stwierdza się odchylenia od linii prostej, przyjmuje się, że reakcja ma rząd ułamkowy, charakterystyczny dla reakcji złożonych^[1][2].

• 

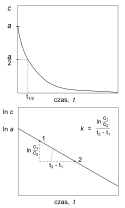
  Krzywe kinetyczne reakcji pierwszego rzędu^[1][2]
  ${\displaystyle c}$ – stężenie substratu, ${\displaystyle a}$ – stężenie początkowe, ${\displaystyle k}$ – stała szybkości reakcji, ${\displaystyle t_{1/2}}$ – czas połowicznej przemiany

• 

  Krzywe kinetyczne reakcji drugiego rzędu^[1][2]
  ${\displaystyle c}$ – stężenie substratu, ${\displaystyle a}$ – stężenie początkowe, ${\displaystyle t_{1/2}}$ – czas połowicznej przemiany

Metoda różnicowa van ’t Hoffa

„Metoda różnicowa” została opracowana przez van ’t Hoffa w 1884 roku. Doświadczalną podstawą obliczeń rzędu reakcji jest w tym przypadku zależność szybkości reakcji w jej początkowym okresie od początkowego stężenia substratu A ${\displaystyle (a).}$

Przyjmuje się, że ogólne równanie kinetyczne^[1][2]:

${\displaystyle -{\frac {dc_{A}}{dt}}=kc_{A}^{n}=k(a-x)^{n}}$

w okresie początkowym ${\displaystyle (x\ll a,\ c_{A}\approx a)}$ można zastąpić przez:

${\displaystyle -{\frac {da}{dt}}=ka^{n}.}$

Dla dwóch reakcji, prowadzonych przy różnych stężeniach początkowych, otrzymuje się:

${\displaystyle -{\frac {da_{1}}{dt}}=ka_{1}^{n},}$

${\displaystyle -{\frac {da_{2}}{dt}}=ka_{2}^{n}.}$

Wynikiem podzielenia równań stronami i zlogarytmowania jest zależność:

${\displaystyle n={\frac {\ln \left(-{\frac {da_{1}}{dt}}\right)-\ln \left(-{\frac {da_{2}}{dt}}\right)}{\ln a_{1}-\ln a_{2}}}}$

lub, po przejściu na skończone wartości przyrostów (${\displaystyle {\text{d}}t\to \Delta t}$ i ${\displaystyle {\text{d}}a\to \Delta a}$):

${\displaystyle n={\frac {\ln \left(-{\frac {\Delta a_{1}}{\Delta t}}\right)-\ln \left(-{\frac {\Delta a_{2}}{\Delta t}}\right)}{\ln a_{1}-\ln a_{2}}}.}$

Metoda całkowa Ostwalda i Zawidzkiego

Podstawą całkowej metody Ostwalda i Zawidzkiego są również wyniki analiz, zgromadzone w dwóch eksperymentach, wykonanych z zastosowaniem różnych wartości początkowego stężenia substratu. W odróżnieniu od metody różnicowej reakcji nie kończy się w okresie początkowym, ale prowadzi do osiągnięcia jednakowego w obu przypadkach stopnia przereagowania (np. zmniejszenie stężenia ${\displaystyle p}$ razy)^[1][2].

Założenia metody ilustrują następujące przekształcenia ogólnego równania kinetycznego (dla reakcji o jednakowych stężeniach substratów):

${\displaystyle -{\frac {dc}{dt}}=kc^{n}}$

• po zgrupowaniu zmiennych:

${\displaystyle -{\frac {dc}{c^{n}}}=kdt}$

• po scałkowaniu w granicach od ${\displaystyle a}$ do ${\displaystyle c}$:

${\displaystyle {\frac {1}{n-1}}\left({\frac {1}{c^{n-1}}}-{\frac {1}{a^{n-1}}}\right)=kt.}$

W przypadku dwóch reakcji, rozpoczynanych od stężeń początkowych ${\displaystyle c=a_{1}}$ i ${\displaystyle c=a_{2}}$ i kończonych na stężeniach ${\displaystyle c=pa_{1}}$ i ${\displaystyle c=pa_{2}}$ otrzymuje się, po uproszczeniach, równania:

${\displaystyle {\frac {1}{n-1}}\cdot {\frac {1-p^{n-1}}{({a_{1}p})^{n-1}}}=kt_{1},}$

${\displaystyle {\frac {1}{n-1}}\cdot {\frac {1-p^{n-1}}{{(a_{2}p)}^{n-1}}}=kt_{2}.}$

Podzielenie obu otrzymanych równań stronami oraz zlogarytmowanie i kolejne przekształcenia prowadzą do zależności umożliwiającej obliczanie rzędu reakcji na podstawie zmierzonych wartości ${\displaystyle t_{1}}$ i ${\displaystyle t_{2}{:}}$

${\displaystyle \left({\frac {a_{2}}{a_{1}}}\right)^{n-1}={\frac {t_{1}}{t_{2}}},}$

${\displaystyle n=1+{\frac {\log {t_{1}}-\log {t_{2}}}{\log {a_{2}}-\log {a_{1}}}}.}$

Metoda izolacyjna Ostwalda

Metodą izolacyjną jest nazywane postępowanie, które umożliwia wyznaczanie rzędu reakcji względem pojedynczych reagentów, np. względem A i B w reakcji A + B → produkty, dla której równanie kinetyczne ma postać:

${\displaystyle -{\frac {dx}{dt}}=k(a-x)_{A}^{n}(b-x)_{B}^{n}.}$

Prowadzenie reakcji przy dużym nadmiarze substratu A umożliwia wyznaczenie rzędu względem substratu B (stężenia A jest uznawane za stałe). Analogicznie wyznacza się rząd względem A, stosując duży nadmiar substratu B. Sumaryczny rząd reakcji jest sumą rzędów względnych^[1][2].

Uwagi

Przypisy